7.7: Ionic and Ion-Derived Solids
- Page ID
- 3582
Make sure you thoroughly understand the following essential ideas which have been presented above.
- What is an ionic solid, what are its typical physical properties, and what kinds of elements does it contain?
- Define the lattice energy of an ionic solid in terms of the energetic properties of its component elements.
- Make a rough sketch that describes the structure of solid sodium chloride.
- Describe the role that the relative ionic radii play in contributing to the stability of an ionic solids.
- Give examples of some solids that can form when ionic solutions are evaporated, but which do not fall into the category of "ionic" solids.
In this section we deal mainly with a very small but important class of solids that are commonly regarded as composed of ions. We will see how the relative sizes of the ions determine the energetics of such compounds. And finally, we will point out that not all solids that are formally derived from ions can really be considered "ionic" at all.
Ionic Solids
The idealized ionic solid consists of two interpenetrating lattices of oppositely-charged point charges that are held in place by a balance of coulombic forces. But because real ions occupy space, no such "perfect" ionic solid exists in nature. Nevertheless, this model serves as a useful starting point for understanding the structure and properties of a small group of compounds between elements having large differences in electronegativity.
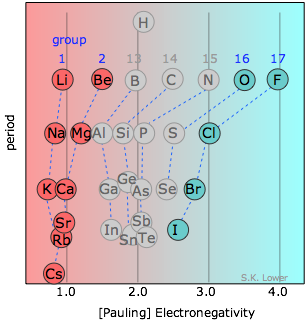
Chemists usually apply the term "ionic solid" to binary compounds of the metallic elements of Groups 1-2 with one of the halogen elements or oxygen. As can be seen from the diagram, the differences in electronegativity between the elements of Groups 1-2 and those of Group 17 (as well as oxygen in Group 16) are sufficiently great that the binding in these solids is usually dominated by Coulombic forces and the crystals can be regarded as built up by aggregation of oppositely-charged ions.
Sodium Chloride (rock-salt) Structure
The most well known ionic solid is sodium chloride, also known by its geological names as rock-salt or halite. We can look at this compound in both structural and energetic terms.

Structurally, each ion in sodium chloride is surrounded and held in tension by six neighboring ions of opposite charge. The resulting crystal lattice is of a type known as simple cubic, meaning that the lattice points are equally spaced in all three dimensions and all cell angles are 90°.
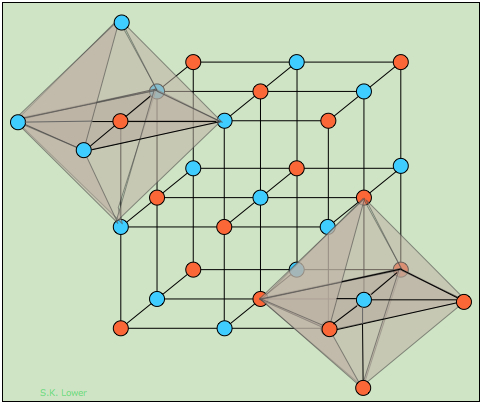
In Figure \(\PageIndex{2}\), we have drawn two imaginary octahedra centered on ions of different kinds and extending partially into regions outside of the diagram. (We could equally well have drawn them at any of the lattice points, but show only two in order to reduce clutter.) Our object in doing this is to show that each ion is surrounded by six other ions of opposite charge; this is known as (6,6) coordination. Another way of stating this is that each ion resides in an octahedral hole within the cubic lattice.
How can one sodium ion surrounded by six chloride ions (or vice versa) be consistent with the simplest formula NaCl? The answer is that each of those six chloride ions also sits at the center of its own octahedron defined by another six sodium ions. You might think that this corresponds to Na6Cl6, but note that the central sodium ion shown in the diagram can claim only a one-sixth share of each of its chloride ion neighbors, so the formula NaCl is not just the simplest formula, but correctly reflects the 1:1 stoichiometry of the compound. But of course, as in all ionic structures, there are no distinguishable "molecular" units that correspond to the NaCl simplest formula. Bear in mind that large amount of empty space in diagrams depicting a crystal lattice structure can be misleading, and that the ions are really in direct contact with each other to the extent that this is geometrically possible.
Sodium Chloride Energetics
Sodium chloride, like virtually all salts, is a more energetically favored configuration of sodium and chlorine than are these elements themselves; in other words, the reaction
\[Na_{(s)} + ½Cl_{2(g)} \rightarrow NaCl_{(s)}\]
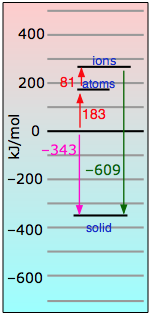
is accompanied by a release of energy in the form of heat. How much heat, and why? To help us understand, we can imagine the formation of one mole of sodium chloride from its elements proceeding in these hypothetical steps in which we show the energies explicitly:
Step 1: Atomization of sodium (breaking one mole of metallic sodium into isolated sodium atoms)
\[\ce{ Na(s) + 108 kJ → Na(g)} \label{Step1}\]
Step 2: Same thing with chlorine. This requires more energy because it involves breaking a covalent bond.
\[\ce{ ½Cl2(g) + 127\, kJ → Cl(g)} \label{Step2}\]
Step 3: We strip an electron from one mole of sodium atoms (this costs a lot of energy!)
\[\ce{ Na(g) + 496\, kJ → Na^{+}(g) + e^{–}} \label{Step3}\]
Step 4: Feeding these electrons to the chlorine atoms gives most of this energy back.
\[\ce{ Cl(g) + e^{–} → Cl^{–}(g) + 348\, kJ}\label{Step4}\]
Step 5: Finally, we bring one mole of the ions together to make the crystal lattice — with a huge release of energy.
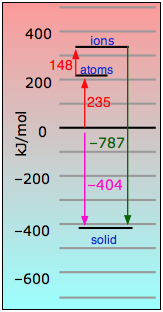
\[\ce{ Na^{+}(g) + Cl^{–}(g) → NaCl(s) + 787\, kJ} \label{Step5}\]
If we add all of these equations together, we get
\[\ce{Na(s) + 1/2Cl2(g) → NaCl(s)} + 404\; kJ\]
In other words, the formation of solid sodium chloride from its elements is highly exothermic. As this energy is released in the form of heat, it spreads out into the environment and will remain unavailable to push the reaction in reverse. We express this by saying that "sodium chloride is more stable than its elements".
Looking at the equations above, you can see that Equation \ref{Step5} constitutes the big payoff in energy. The 787 kj/mol noted there is known as the NaCl lattice energy. Its large magnitude should be no surprise, given the strength of the coulombic force between ions of opposite charge.
It turns out that it is the lattice energy that renders the gift of stability to all ionic solids.Note that this lattice energy, while due principally to coulombic attraction between each ion and its eight nearest neighbors, is really the sum of all the interactions with the crystal. Lattice energies cannot be measured directly, but they can be estimated fairly well from the energies of the other processes described in the table immediately above.
How Geometry and Periodic Properties Interact
The most energetically stable arrangement of solids made up of identical molecular units (as in the noble gas elements and pure metals) are generally those in which there is a minimum of empty space; these are known as close-packed structures, and there are several kinds. In the case of ionic solids of even the simplest 1:1 stoichiometry, the positive and negative ions usually differ so much in size that packing is often much less efficient. This may cause the solid to assume lattice geometries that differ from the one illustrated above for sodium chloride.
By way of illustration, consider the structure of cesium chloride (the spelling cæsium is also used), CsCl. The radius of the Cs+ ion is 168 pm compared to 98 pm for Na+ and cannot possibly fit into the octahedral hole of a simple cubic lattice of chloride ions. The CsCl lattice therefore assumes a different arrangement.
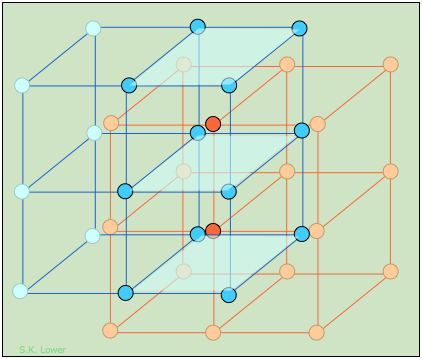
Figure \(\PageIndex{3}\) focuses on two of these cubic lattice elements whose tops and bottoms are shaded for clarity. It should be easy to see that each cesium ion now has eight nearest-neighbor chloride ions. Each chloride ion is also surrounded by eight cesium ions, so all the lattice points are still geometrically equivalent. We therefore describe this structure as having (8,8) coordination.
The two kinds of lattice arrangements exemplified by NaCl ("rock salt") and CsCl are found in a large number of other 1:1 ionic solids, and these names are used generically to describe the structures of these other compounds. There are of course many other fundamental lattice arrangements (not all of them cubic), but the two we have described here are sufficient to illustrate the point that the radius ratio (the ratio of the radii of the positive to the negative ion) plays an important role in the structures of simple ionic solids.
The Alkali Halides
The interaction of the many atomic properties that influence ionic binding are nicely illustrated by looking at a series of alkali halides, especially those involving extreme differences in atomic radii. The latter are all drawn to the same scale. On the energetic plots at the right, the lattice energies are shown in green. We will start with the one you already know very well.
|
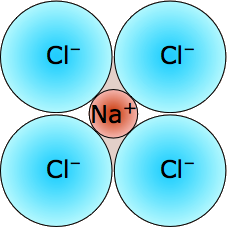
Sodium chloride - NaCl ("rock-salt") mp/bp 801/1413 °C; coordination (6,6) |
 |
 |
|
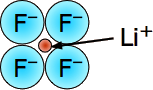
Lithium Fluoride - LiF - mp/bp 846/1676 °C, rock-salt lattice structure (6,6). Tiny-tiny makes strong-strong! This is the most "ionic" of the alkali halides, with the largest lattice energy and highest melting and boiling points. The small size of these ions (and consequent high charge densities) together with the large electronegativity difference between the two elements places a lot of electronic charge between the atoms. Even in this highly ionic solid, the electron that is "lost" by the lithium atom turns out to be closer to the Li nucleus than when it resides in the 2s shell of the neutral atom. |
 |
 |
|
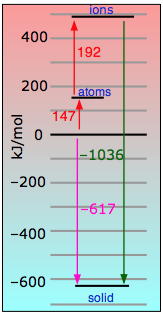
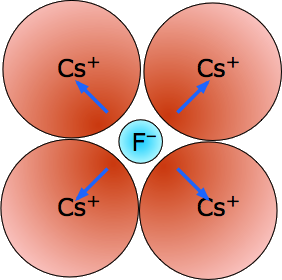
Cesium Fluoride, CsF - mp/bp 703/1231 °C, (8,8) coordination. With five shells of electrons shielding its nucleus, the Cs+ ion with its low charge density resembles a big puff-ball which can be distorted by the highly polarizing fluoride ion. The resulting ion-induced dipoles (blue arrows) account for much of the lattice energy here. The reverse of this would be a tiny metal ion trying to hold onto four relatively huge iodide ions like Lithium iodide. |
 |
 |
|
Lithium iodide, LiI - mp/bp 745/1410 °C. Negative ions can make even bigger puff-balls. The tiny lithium ion can't get very close to any of the iodides to generate a very strong coulombic binding, but does polarize them to create an ion-induced dipole component. It does not help that the negative ions are in contact with each other. The structural geometry is the same (6,6) coordination as NaCl. |
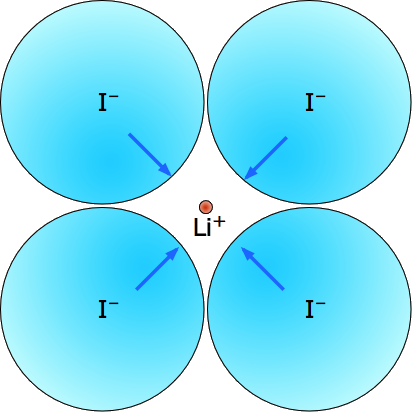 |
 |
|
Cesium iodide, CsI - mp/bp 626/1280 °C. Even with the (8,8) coordination afforded by the CsCl structure, this is a pretty sorry combination owing to the low charge densities. The weakness of coulombic- compared to van der Waals interactions makes this the least-"ionic" of all the alkali halide solids. |
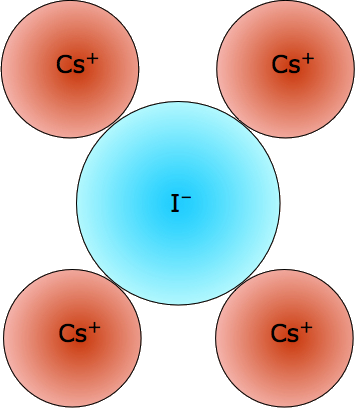 |
 |
Conclusion: Many of the alkali halide solids are not all that "ionic" in the sense that coulombic forces are the predominant actors; in many, such as the CsI illustrated above, ion-induced dipole forces are more important.
Some Properties of Ionic Solids
As noted above, ionic solids are generally hard and brittle. Both of these properties reflect the strength of the coulombic force. Hardness measures resistance to deformation. Because the ions are tightly bound to their oppositely-charged neighbors and, a mechanical force exerted on one part of the solid is resisted by the electrostatic forces operating over an extended volume of the crystal.
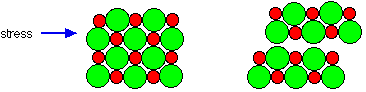
But by applying sufficient force, one layer of ions can be made to slip over another; this is the origin of brittleness. This slippage quickly propagates along a plane of the crystal (more readily in some directions than in others), weakening their attraction and leading to physical cleavage. Because the "ions" in ionic solids lack mobility, the solids themselves are electrical insulators.
Not all ion-derived solids are "ionic".
Even within the alkali halides, the role of coulombic attraction diminishes as the ions become larger and more polarizable or differ greatly in radii. This is especially true of the anions, which tend to be larger and whose electron clouds are more easily distorted. In solids composed of polyatomic ions such as (NH4)2SO4, SrClO4, NH4CO3, ion-dipole and ion-induced dipole forces may actually be stronger than the coulombic force. Higher ionic charges help, especially if the ions are relatively small. This is especially evident in the extremely high melting points of the Group 2 and higher oxides:
| MgO (magnesia) | CaO (lime) | SrO (strontia) | Al2O3 (alumina) | ZrO2 (zirconia) |
|---|---|---|---|---|
| 2830 °C | 2610 °C | 2430 °C | 2050 °C | 2715 °C |
These substances are known as refractories, meaning that they retain their essential properties at high temperatures. Magnesia, for example, is used to insulate electric heating elements and, in the form of fire bricks, to line high-temperature furnaces. No boiling points have been observed for these compounds; on further heating, they simply dissociate into their elements. Their crystal structures can be very complex, and some (notably Al2O3) can have several solid forms. Even in the most highly ionic solids there is some electron sharing, so the idea of a “pure” ionic bond is an abstraction.
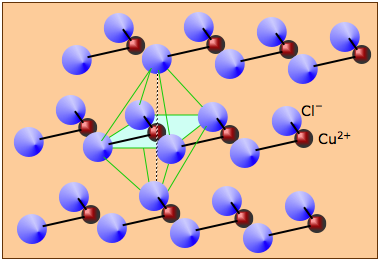
Many solids that are formally derived from ions cannot really be said to form "ionic" solids at all. For example, anhydrous copper(II) chloride consists of layers of copper atoms surrounded by four chlorine atoms in a square arrangement. Neighboring chains are offset so as to create an octahedral coordination of each copper atom. Similar structures are commonly encountered for other salts of transition metals. Similarly, most oxides and sulfides of metals beyond Group 2 tend to have structures dominated by other than ion-ion attractions.
The trihalides of aluminum offer another example of the dangers of assuming ionic character of solids that are formally derived from ions. Aqueous solutions of what we assume to be AlF3, AlCl3, AlBr3, and AlI3 all exhibit the normal properties ionic solutions (they are electrically conductive, for example), but the solids are quite different: the melting point of AlF3 is 1290°C, suggesting that it is indeed ionic. But AlCl3 melts at 192°C — hardly consistent with ionic bonding, and the other two halides are also rather low-melting. Structural studies show that when AlCl3 vaporizes or dissolves in a non-polar solvent it forms a dimer Al2Cl6. The two other halides exist only as dimers in all states.
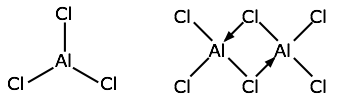
The structural formula of the Al2Cl6 molecule shows that the aluminum atoms are bonded to four chlorines, two of which are shared between the two metal atoms. The arrows represent coordinate covalent bonds in which the bonding electrons both come from the same atom (chlorine in this case.)
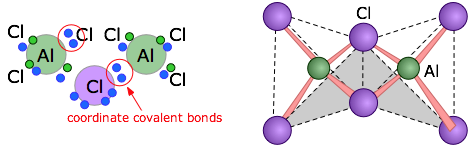
As shown at the right above, the aluminum atoms can be considered to be located at the centers of two tetrahedra that possess one edge in common.


