5.6: Atomic Electron Configurations
- Page ID
- 3502
Make sure you thoroughly understand the following essential ideas:
- State the principle feature of that distinguishes the energies of the excited states of a single-electron atom from atoms containing more than one electron.
- Explain why the first ionization energy of the helium atom is smaller than twice the first ionization of the hydrogen atom.
- Be able to write a plausible electron configuration for any atom having an atomic number less than 90.
In the previous section you learned that an electron standing-wave pattern characterized by the quantum numbers (n,l,m) is called an orbital. According to the Pauli exclusion principle, no two electrons in the same atom can have the same set of quantum numbers (n,l,m,s). This limits the number of electrons in a given orbital to two (s = ±1), and it requires that atom containing more then two electrons must place them in standing wave patterns corresponding to higher principal quantum numbers n, which means that these electrons will be farther from the nucleus and less tightly bound by it.
In this chapter, we will see how the Pauli restrictions on the allowable quantum numbers of electrons in an atom affect the electronic configuration of the different elements, and, by influencing their chemical behavior, governs the structure of the periodic table.
One-electron atoms
Let us begin with atoms that contain only a single electron. Hydrogen is of course the only electrically neutral species of this kind, but by removing electrons from heavier elements we can obtain one-electron ions such as \(He^+\) and \(Li^{2+}\), etc. Each has a ground state configuration of 1s1, meaning that its single electron exhibits a standing wave pattern governed by the quantum numbers n=1, m=0 and l=0, with the spin quantum number s undefined because there is no other electron to compare it with. All have simple emission spectra whose major features were adequately explained by Bohr's model.
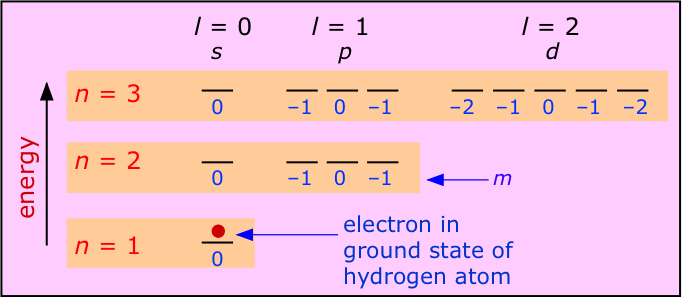
The most important feature of a single-electron atom is that the energy of the electron depends only on the principal quantum number n. As the above diagram shows, the quantum numbers l and m have no effect on the energy; we say that all orbitals having a given value of n are degenerate. Thus the emission spectrum produced by exciting the electron to the n=2 level consists of a single line, not four lines. The wavelength of this emission line for the atoms H, He+and Li2+ will diminish with atomic number because the greater nuclear charge will lower the energies of the various n levels. For the same reason, the energies required to remove an electron from these species increases rapidly as the nuclear charge increases, because the increasing attraction pulls the electron closer to the nucleus, thus producing an even greater attractive force.
Electron-Electron Repulsion
It takes 1312 kJ of energy to remove the electron from a mole of hydrogen atoms. What might we expect this value to be for helium? Helium contains two electrons, but its nucleus contains two protons; each electron "sees" both protons, so we might expect that the electrons of helium would be bound twice as strongly as the electron of hydrogen. The ionization energy of helium should therefore be twice 1312 kJ/mol, or 2612 kJ/mol. However, if one looks at the spectrum of helium, the continuum is seen to begin at a wavelength corresponding to an ionization energy of 2372 kJ/mol, or about 90% of the predicted value.
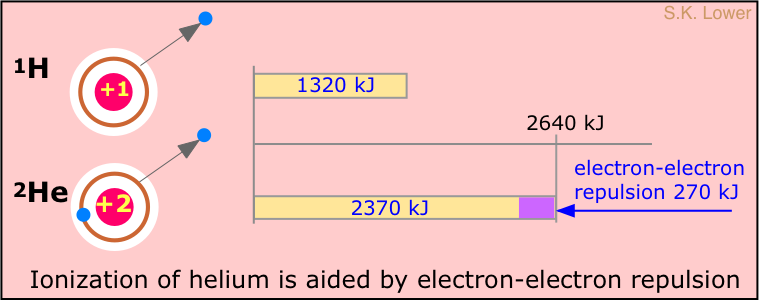
Why are the electrons in helium bound less tightly than the +2 nuclear charge would lead us to expect? The answer is that there is another effect to consider: the repulsion between the two electrons; the resulting electron-electron repulsion subtracts from the force holding the electron to the nucleus, reducing the local binding of each.
Electron-electron repulsion is a major factor in both the spectra and chemical behavior of the elements heavier than hydrogen. In particular, it acts to "break the degeneracy" (split the energies) of orbitals having the same value of n but different l.
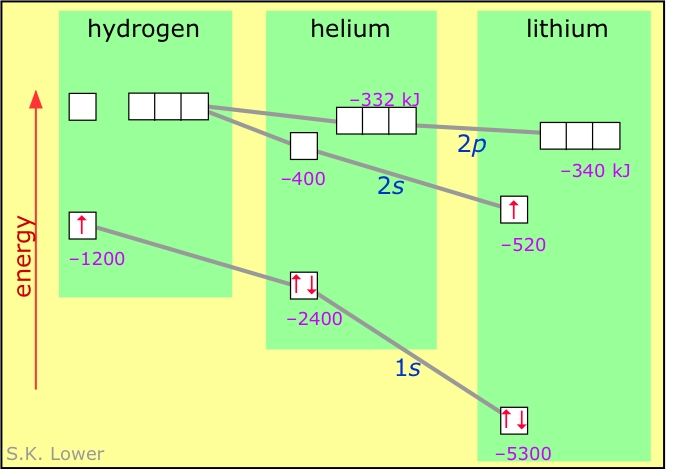
The diagram below shows how the energies of the s- and p-orbitals of different principal quantum numbers get split as the result of electron-electron repulsion. Notice the contrast with the similar diagram for one-electron atoms near the top of this page. The fact that electrons preferentially fill the lowest-energy empty orbitals is the basis of the rules for determining the electron configuration of the elements and of the structure of the periodic table.
The Aufbau rules
The German word Aufbau means "building up", and this term has traditionally been used to describe the manner in which electrons are assigned to orbitals as we carry out the imaginary task of constructing the atoms of elements having successively larger atomic numbers. In doing so, we are effectively "building up" the periodic table of the elements, as we shall shortly see.
How to play the Aufbau game- Electrons occupy the lowest-energy available orbitals; lower-energy orbitals are filled before the higher ones.
- No more than two electrons can occupy any orbital.
- For the lighter elements, electrons will fill orbitals of the same type only one electron at a time, so that their spins are all unpaired. They will begin to pair up only after all the orbitals are half-filled. This principle, which is a consequence of the electrostatic repulsion between electrons, is known as Hund's rule.
- For the first 18 elements, up to the point where the 3s and 3p levels are completely filled, this scheme is entirely straightforward and leads to electronic configurations which you are expected to be able to work out for each of these elements.
The preceding diagram illustrates the main idea here. Each orbital is represented as a little box that can hold up to two electrons having opposite spins, which we designated by upward- or downward-pointing arrows. Electrons fill the lowest-energy boxes first, so that additional electrons are forced into wave-patterns corresponding to higher (less negative) energies. Thus in the above diagram, the "third" electron of lithium goes into the higher-energy 2s orbital, giving this element an electron configuration which we write 1s2 2s1.
What is the electron configuration of the atom of phosphorus, atomic number 15?
The number of electrons filling the lowest-energy orbitals are:
1s: 2 electrons, 2s: 2 electrons; 2p: 6 electrons, 3s: 2 electrons. This adds up to 12 electrons. The remaining three electrons go into the 3p orbital, so the complete electron configuration of P is 1s2 2s2 2p6 3s2 3p3.
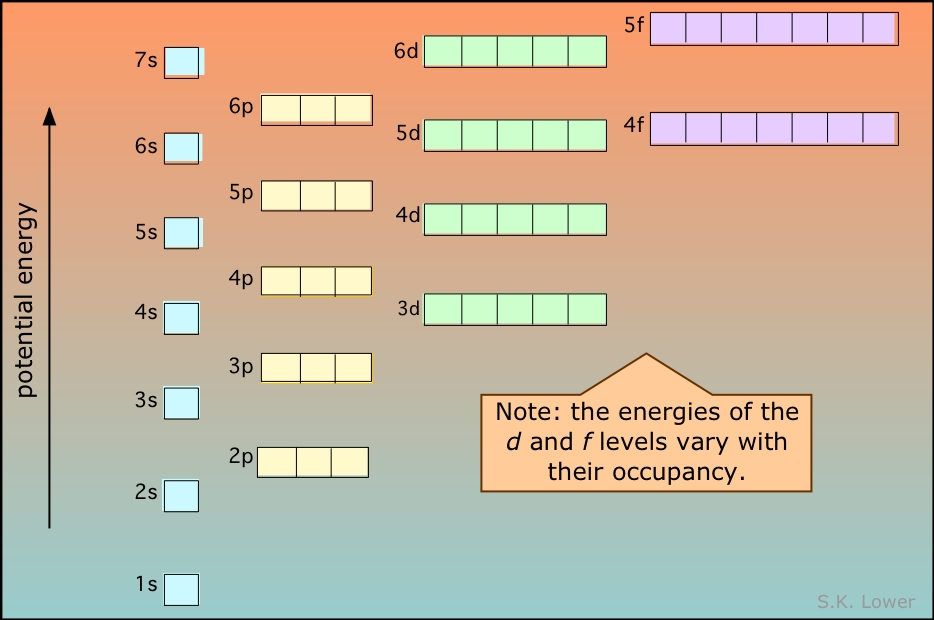
Energies of the highest occupied orbitals of the elements: This diagram illustrates the Aufbau rules as they are applied to all the elements. Note especially how the energies of the nd orbitals fall between the (n–1)s and (n–1)p orbitals so, for example the 3d orbitals begin to fill after the 4s orbital is filled, but before electrons populate the 4p orbitals. A similar relation exists with d- and f-orbitals.
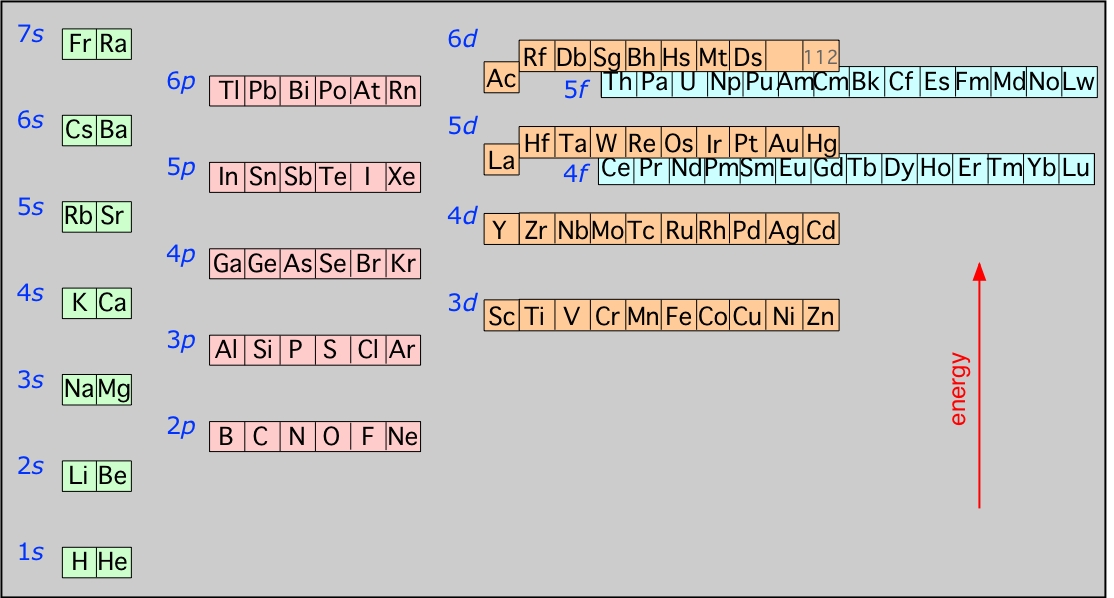
It is very important that you understand this diagram and how it follows from the Pauli exclusion principle: You should be able to reproduce it from memory up to the 6s level, because it forms the fundamental basis of the periodic table of the elements.
Bending the rules
Inspection of a table of electron configurations of the elements reveals a few apparent non-uniformities in the filling of the orbitals, as is illustrated here for the elements of the so-called first transition series in which the 3d orbitals are being populated. These anomalies are a consequence of the very small energy differences between some of the orbitals, and of the reduced electron-electron repulsion when electrons remain unpaired (Hund's rule), as is evident in chromium, which contains six unpaired electrons.
The other anomaly here is copper, which "should" have the outer-shell configuration 3d94s2. The actual configuration of the Cu atom appears to be 3d104s1. Although the 4s orbital is normally slightly below the 3d orbital energy, the two are so close that interactions between the two when one is empty and the other is not can lead to a reversal. Detailed calculations in which the shapes and densities of the charge distributions are considered predict that the relative energies of many orbitals can reverse in this way. It gets even worse when f-orbitals begin to fill!
Because these relative energies can vary even for the same atom in different chemical environments, most instructors will not expect you to memorize them.
This diagram shows how the atomic orbitals corresponding to different principal quantum numbers become interspersed with one another at higher values of n. The actual situation is more complicated than this; calculations show that the energies of d and f orbitals vary with the atomic number of the element.
The Periodic Table
The relative orbital energies illustrated above and the Pauli exclusion principle constitute the fundamental basis of the periodic table of the elements which was of course worked out empirically late in the 19th century, long before electrons had been heard of.
The periodic table of the elements is conventionally divided into sections calledblocks, each of which designates the type of "sub-orbital" (s, p, d, f) which contains the highest-energy electrons in any particular element. Note especially that
- The non-metallic elements occur only in the p-block;
- The d-block elements contain the so-called transition elements;
- The f-block elements go in between Groups 3 and 4 of the d-block.
The above diagram illustrates the link between the electron configurations of the elements and the layout of the periodic table. Each row, also known as a period, commences with two s-block elements and continues through the p block. At the end of the rows corresponding to n>1 is an element having a p6 configuration, a so-called noble gas element. At n values of 2 and 3, d- and f-block element sequences are added.
The table shown above is called the long form of the periodic table; for many purposes, we can use a "short form" table in which the d-block is shown below the s- and p- block "representative elements" and the f-block does not appear at all. Note that the "long form" would be even longer if the f-block elements were shown where they actually belong, between La-Hf and Ac-Db.


