5.3: Light, Particles, and Waves
- Page ID
- 3503
Make sure you thoroughly understand the following essential ideas
- Cite two pieces of experimental evidence that demonstrate, respectively, the wave- and particle-like nature of light.
- Define the terms amplitude, wavelength, and frequency as they apply to wave phenomena.
- Give a qualitative description of electromagnetic radiation in terms of electrostatic and magnetic fields.
- Be able to name the principal regions of the electromagnetic spectrum (X-rays, infrared region, etc.) and specify their sequence in terms of either wavelength or energy per photon.
- Describe the difference between line spectra and continuous spectra in terms of both their appearance and their origins.
- What is meant by the de Broglie wavelength of a particle? How will the particle's mass and velocity affect the wavelength?
- State the consequences of the Heisenberg uncertainty principle in your own words.
Our intuitive view of the "real world" is one in which objects have definite masses, sizes, locations and velocities. Once we get down to the atomic level, this simple view begins to break down. It becomes totally useless when we move down to the subatomic level and consider the lightest of all chemically-significant particles, the electron. The chemical properties of a particular kind of atom depend on the arrangement and behavior of the electrons which make up almost the entire volume of the atom. The electronic structure of an atom can only be determined indirectly by observing the manner in which atoms absorb and emit light. Light, as you already know, has wavelike properties, so we need to know something about waves in order to interpret these observations. But because the electrons are themselves quantum particles and therefore have wavelike properties of their own, we will find that an understanding of the behavior of electrons in atoms can only be gained through the language of waves.
The language of light
Atoms are far too small to see directly, even with the most powerful optical microscopes. But atoms do interact with and under some circumstances emit light in ways that reveal their internal structures in amazingly fine detail. It is through the "language of light" that we communicate with the world of the atom. This section will introduce you to the rudiments of this language.
Wave, particle, or what?
In the early 19th century, the English scientist Thomas Young carried out the famous double-slit experiment which demonstrated that a beam of light, when split into two beams and then recombined, will show interference effects that can only be explained by assuming that light is a wavelike disturbance. By 1820, Augustin Fresnel had put this theory on a sound mathematical basis, but the exact nature of the waves remained unclear until the 1860's when James Clerk Maxwell developed his electromagnetic theory.
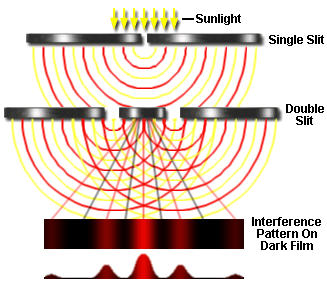
But Einstein's 1905 explanation of the photoelectric effect showed that light also exhibits a particle-like nature. The photon is the smallest possible packet (quantum) of light; it has zero mass but a definite energy.
When light-wave interference experiments are conducted with extremely low intensities of light, the wave theory breaks down; instead of recording a smooth succession of interference patterns as shown above, an extremely sensitive detector sees individual pulses— that is, individual photons.
Note
Suppose we conduct the double-slit interference experiment using a beam of light so weak that only one photon at a time passes through the apparatus (it is experimentally possible to count single photons, so this is a practical experiment.) Each photon passes through the first slit, and then through one or the other of the second set of slits, eventually striking the photographic film where it creates a tiny dot. If we develop the film after a sufficient number of photons have passed through, we find the very same interference pattern we obtained with higher-intensity light whose behavior was could be explained by wave interference.
There is something strange here. Each photon, acting as a particle, must pass through one or the other of the pair of slits, so we would expect to get only two groups of spots on the film, each opposite one of the two slits. Instead, it appears that the each particle, on passing through one slit, "knows" about the other, and adjusts its final trajectory so as to build up a wavelike interference pattern.
It gets even stranger: suppose that we set up a detector to determine which slit a photon is heading for, and then block off the other slit with a shutter. We find that the photon sails straight through the open slit and onto the film without trying to create any kind of an interference pattern. Apparently, any attempt to observe the photon as a discrete particle causes it to behave like one.
One well-known physicist (Landé) suggested that perhaps we should coin a new word, wavicle, to reflect this duality.
Later on, virtually the same experiment was repeated with electrons, thus showing that particles can have wavelike properties (as the French physicist Louis de Broglie predicted in 1923), just as what were conventionally thought to be electromagnetic waves possess particle-like properties.
Is it a particle or is it a wave?
For large bodies (most atoms, baseballs, cars) there is no question: the wave properties are insignificant, and the laws of classical mechanics can adequately describe their behaviors. But for particles as tiny as electrons (quantum particles), the situation is quite different: instead of moving along well defined paths, a quantum particle seems to have an infinity of paths which thread their way through space, seeking out and collecting information about all possible routes, and then adjusting its behavior so that its final trajectory, when combined with that of others, produces the same overall effect that we would see from a train of waves of wavelength = h/mv.

Taking this idea of quantum indeterminacy to its most extreme, the physicist Erwin Schrödinger proposed a "thought experiment" in which the radioactive decay of an atom would initiate a chain of events that would lead to the death of a cat placed in a closed box. The atom has a 50% chance of decaying in an hour, meaning that its wave representation will contain both possibilities until an observation is made. The question, then, is will the cat be simultaneously in an alive-and-dead state until the box is opened? If so, this raises all kinds of interesting questions about the nature of being.
What you need to know about waves
We use the term "wave" to refer to a quantity which changes with time. Waves in which the changes occur in a repeating or periodic manner are of special importance and are widespread in nature; think of the motions of the ocean surface, the pressure variations in an organ pipe, or the vibrations of a plucked guitar string. What is interesting about all such repeating phenomena is that they can be described by the same mathematical equations.
Wave motion arises when a periodic disturbance of some kind is propagated through a medium; pressure variations through air, transverse motions along a guitar string, or variations in the intensities of the local electric and magnetic fields in space, which constitutes electromagnetic radiation. For each medium, there is a characteristic velocity at which the disturbance travels.
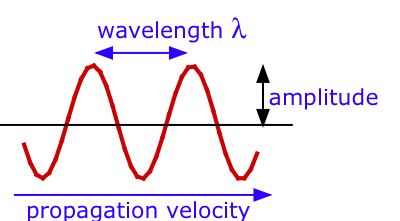
There are three measurable properties of wave motion: amplitude,wavelength, and frequency, the number of vibrations per second. The relation between the wavelength \(λ\) (Greek lambda) and frequency of a wave \( u\) (Greek nu) is determined by the propagation velocity v.
\[v = u λ\]
What is the wavelength of the musical note A = 440 hz when it is propagated through air in which the velocity of sound is 343 m s–1?
Solution
\[λ = \dfrac{v} { u} = \dfrac{343\; m \,s^{–1}}{440\, s^{–1}} = 0.80\; m\]
Light and electromagnetic radiation
Michael Faraday's discovery that electric currents could give rise to magnetic fields and vice versa raised the question of how these effects are transmitted through space. Around 1870, the Scottish physicist James Clerk Maxwell (1831-1879) showed that this electromagnetic radiation can be described as a train of perpendicular oscillating electric and magnetic fields.

Maxwell was able to calculate the speed at which electromagnetic disturbances are propagated, and found that this speed is the same as that of light. He therefore proposed that light is itself a form of electromagnetic radiation whose wavelength range forms only a very small part of the entire electromagnetic spectrum. Maxwell's work served to unify what were once thought to be entirely separate realms of wave motion.
The electromagnetic spectrum
The electromagnetic spectrum is conventionally divided into various parts as depicted in the diagram below, in which the four logarithmic scales correlate the wavelength of electromagnetic radiation with its frequency in herz (units of s–1) and the energy per photon, expressed both in joules and electron-volts.
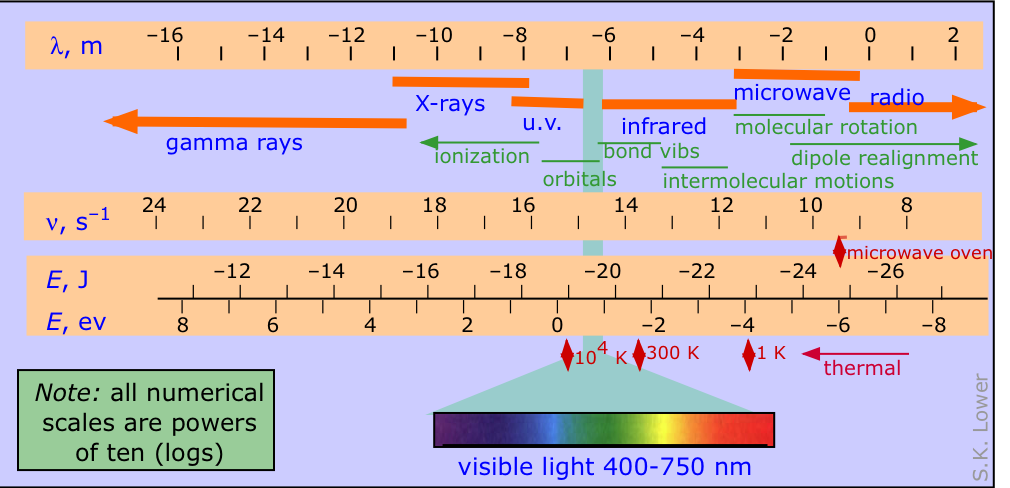
The other items shown on the diagram, from the top down, are:
- the names used to denote the various wavelength ranges of radiation (you should know their names and the order in which they appear)
- the principal effects of the radiation on atoms and molecules
- the peaks of thermal radiation emitted by black bodies at three different temperatures
Electromagnetic radiation and chemistry. It's worth noting that radiation in the ultraviolet range can have direct chemical effects by ionizing atoms and disrupting chemical bonds. Longer-wavelength radiation can interact with atoms and molecules in ways that provide a valuable means of identifying them and revealing particular structural features.
Energy units and magnitudes
It is useful to develop some feeling for the various magnitudes of energy that we must deal with. The basic SI unit of energy is the Joule; the appearance of this unit in Planck's constant h allows us to express the energy equivalent of light in joules. For example, light of wavelength 500 nm, which appears blue-green to the human eye, would have a frequency of
The quantum of energy carried by a single photon of this frequency is
Another energy unit that is commonly employed in atomic physics is the electron volt; this is the kinetic energy that an electron acquires upon being accelerated across a 1-volt potential difference. The relationship 1 eV = 1.6022E–19 J gives an energy of 2.5 eV for the photons of blue-green light.
Two small flashlight batteries will produce about 2.5 volts, and thus could, in principle, give an electron about the same amount of kinetic energy that blue-green light can supply. Because the energy produced by a battery derives from a chemical reaction, this quantity of energy is representative of the magnitude of the energy changes that accompany chemical reactions.
In more familiar terms, one mole of 500-nm photons would have an energy equivalent of Avogadro's number times 4E–19 J, or 240 kJ per mole. This is comparable to the amount of energy required to break some chemical bonds. Many substances are able to undergo chemical reactions following light-induced disruption of their internal bonding; such molecules are said to be photochemically active.
Spectra: Interaction of light and matter
Continuous spectra
Any body whose temperature is above absolute zero emits radiation covering a broad range of wavelengths. At very low temperatures the predominant wavelengths are in the radio microwave region. As the temperature increases, the wavelengths decrease; at room temperature, most of the emission is in the infrared.
At still higher temperatures, objects begin to emit in the visible region, at first in the red, and then moving toward the blue as the temperature is raised. These thermal emission spectra are described as continuous spectra, since all wavelengths within the broad emission range are present.

The source of thermal emission most familiar to us is the Sun. When sunlight is refracted by rain droplets into a rainbow or by a prism onto a viewing screen, we see the visible part of the spectrum.
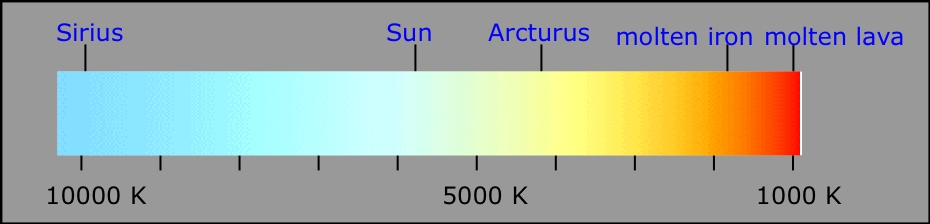
Red hot, white hot, blue hot... your rough guide to temperatures of hot objects.
Line spectra
Heat a piece of iron up to near its melting point and it will emit a broad continuous spectrum that the eye perceives as orange-yellow. But if you zap the iron with an electric spark, some of the iron atoms will vaporize and have one or more of their electrons temporarily knocked out of them. As they cool down the electrons will re-combine with the iron ions, losing energy as the move in toward the nucleus and giving up this excess energy as light. The spectrum of this light is anything but continuous; it consists of a series of discrete wavelengths which we call lines.
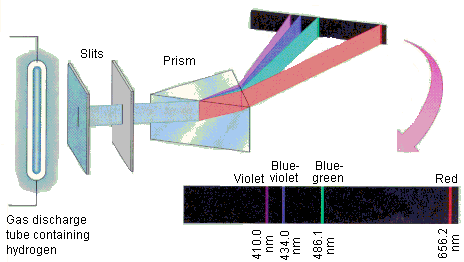
Each chemical element has its own characteristic line spectrum which serves very much like a "fingerprint" capable of identifying a particular element in a complex mixture. Shown below is what you would see if you could look at several different atomic line spectra directly.
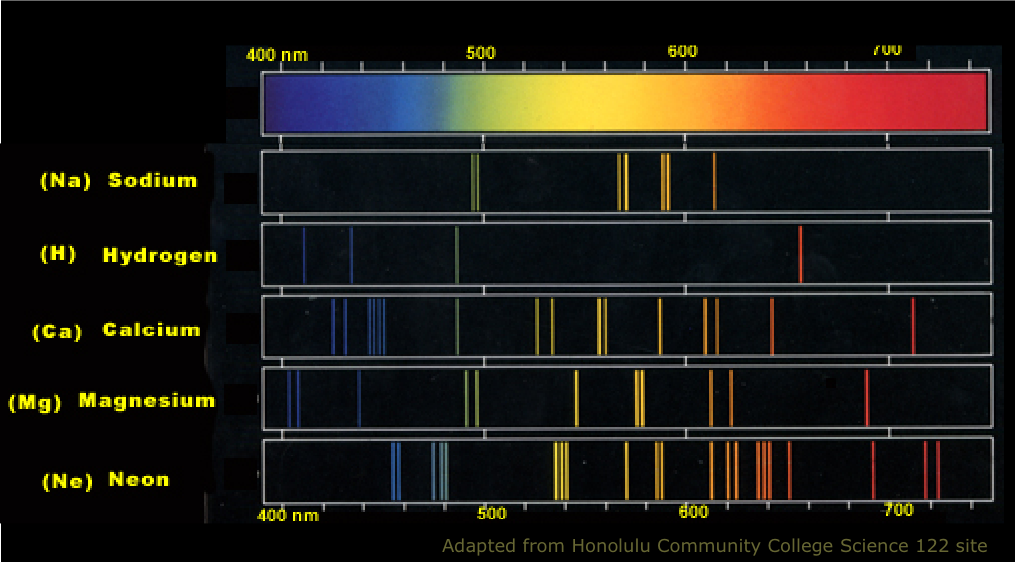
Atomic line spectra are extremely useful for identifying small quantities of different elements in a mixture.
- Companies that own large fleets of trucks and buses regularly submit their crankcase engine oil samples to spectrographic analysis. If they find high levels of certain elements (such as vanadium) that occur only in certain alloys, this can signal that certain parts of the engine are undergoing severe wear. This allows the mechanical staff to take corrective action before engine failure occurs.
- Several elements (Rb, Cs, Tl) were discovered by observing spectral lines that did not correspond to any of the then-known elements. Helium, which is present only in traces on Earth, was first discovered by observing the spectrum of the Sun.
- A more prosaic application of atomic spectra is determination of the elements present in stars.
If you live in a city, you probably see atomic line light sources every night! "Neon" signs are the most colorful and spectacular, but high-intensity street lighting is the most widespread source. A look at the emission spectrum (above) of sodium explains the intense yellow color of these lamps. The spectrum of mercury (not shown) similarly has its strongest lines in the blue-green region.
Particles and waves
There is one more fundamental concept you need to know before we can get into the details of atoms and their spectra. If light has a particle nature, why should particles not possess wavelike characteristics? In 1923 a young French physicist, Louis de Broglie, published an argument showing that matter should indeed have a wavelike nature. The de Broglie wavelength of a body is inversely proportional to its momentum mv:
\[ \lambda =\dfrac{h}{mv}\]
If you explore the magnitude of the quantities in this equation (recall that h is around 10–33 J s), it will be apparent that the wavelengths of all but the lightest bodies are insignificantly small fractions of their dimensions, so that the objects of our everyday world all have definite boundaries. Even individual atoms are sufficiently massive that their wave character is not observable in most kinds of experiments. Electrons, however, are another matter; the electron was in fact the first particle whose wavelike character was seen experimentally, following de Broglie's prediction. Its small mass (9.1E–31 kg) made it an obvious candidate, and velocities of around 100 km/s are easily obtained, yielding a value of λ in the above equation that well exceeds what we think of as the "radius" of the electron. At such velocities the electron behaves as if it is "spread out" to atomic dimensions; a beam of these electrons can be diffracted by the ordered rows of atoms in a crystal in much the same way as visible light is diffracted by the closely-spaced groves of a CD recording.
Electron diffraction has become an important tool for investigating the structures of molecules and of solid surfaces.
A more familiar exploitation of the wavelike properties of electrons is seen in the electron microscope, whose utility depends on the fact that the wavelength of the electrons is much less than that of visible light, thus allowing the electron beam to reveal detail on a correspondingly smaller scale.
The uncertainty principle
In 1927, the German physicist Werner Heisenberg pointed out that the wave nature of matter leads to a profound and far-reaching conclusion: no method of observation, however perfectly it is carried out, can reveal both the exact location and momentum (and thus the velocity) of a particle. This is the origin of the widely known concept that the very process of observation will change the value of the quantity being observed. The Heisenberg principle can be expressed mathematically by the inequality
\[ \Delta{x}\Delta{p} \leq \dfrac{h}{2\pi}\]
in which the \(\Delta\) (deltas) represent the uncertainties with which the location and momentum are known.
Note
Suppose that you wish to measure the exact location of a particle that is at rest (zero momentum). To accomplish this, you must "see" the molecule by illuminating it with light or other radiation. But the light acts like a beam of photons, each of which possesses the momentum h/λ in which λ is the wavelength of the light. When a photon collides with the particle, it transfers some of its momentum to the particle, thus altering both its position and momentum.
Notice how the form of this expression predicts that if the location of an object is known exactly (\(\Delta{x} = 0\)), then the uncertainty in the momentum must be infinite, meaning that nothing at all about the velocity can be known. Similarly, if the velocity were specified exactly, then the location would be entirely uncertain and the particle could be anywhere. One interesting consequence of this principle is that even at a temperature of absolute zero, the molecules in a crystal must still possess a small amount of zero point vibrational motion, sufficient to limit the precision to which we can measure their locations in the crystal lattice.
An equivalent formulation of the uncertainty principle relates the uncertainties associated with a measurement of the energy of a system to the time \(\Delta{t}\) taken to make the measurement:
\[ \Delta{E}\Delta{t} \leq \dfrac{h}{2 \pi}\]
The "uncertainty" referred to here goes much deeper than merely limiting our ability to observe the quantity \(\Delta{x}\Delta{p}\) to a greater precision than \(h/2\pi\). It means, rather, that this product has no exact value, nor, by extension, do position and momentum on a microscopic scale. A more appropriate term would be indeterminacy, which is closer to Heisenberg's original word Ungenauigkeit.
The revolutionary nature Heisenberg's uncertainty principle soon extended far beyond the arcane world of physics; its consequences quickly entered the realm of ideas and has inspired numerous creative works in the arts— few of which really have much to do with the Principle! A possible exception is Michael Frayn's widely acclaimed play (see below) that has brought a sense of Heisenberg's thinking to a wide segment of the public.


