17.3: The Second Commandment
- Page ID
- 285408
GIVEN THAT THE BURDEN UPON EARTH’SSUPPORT SYSTEM IS THE PRODUCT OF NUMBER OF PEOPLE TIMES DEMAND PER PERSON, IT IS ESSENTIAL TO ADDRESS BOTH NUMBERS OF PEOPLE ON EARTH AND THE DEMAND THAT EACH PUTS ON EARTH’S RESOURCES
The burden placed upon Earth’s support systems can be expressed by the equation
\[\textrm{Burden = (Number of people)} \times \textrm{(Demand per person)}\]
This equation shows that both the number of people and the demand that each puts on Earth’sresources must be considered in reducing the impact of humans on Earth. Both must be addressed to achieve sustainability.
As of 2010, Earth’s human population approached 7 billion people and that of the U.S. stood at approximately 308 million people. Numbers of people on Earth will be controlled eventually by one way or another. Studies of natural ecosystems show that increases in population beyond an ecosystem’s carrying capacity are always followed by a population crash; the same principle applies to human populations. Although improved food crop productivity and other measures have so far averted the catastrophic starvation that some experts were predicting in the 1960s, these humane practices have simply delayed the massive population crash that inevitably will occur if population continues to grow.
There is some good news (or perhaps less bad news) regarding population in that the population increase is significantly below that suggested by projections made 40 or 50 years earlier. Even in developing countries, birth rates have fallen to significantly lower levels than expected earlier. Particularly in Italy, Spain, France, and other nations in Europe, birth rates have fallen to appreciably below the replacement level and there is concern over depopulation. Even in the U.S., the birth rate has fallen below replacement levels and population growth that is taking place is the result of immigration. The increase in world population that has occurred over the last half century has been more due to decreasing death rates than to increasing birth rates. One U.N.official opined that, “It is not so much that people started reproducing like rabbits that they stopped dying like flies!” Although these trends do not justify complacency—population growth rates globally and in the world as a whole are still too high—they provide room for some encouragement and give hope that the first factor in Equation 17.3.1 may be controlled.
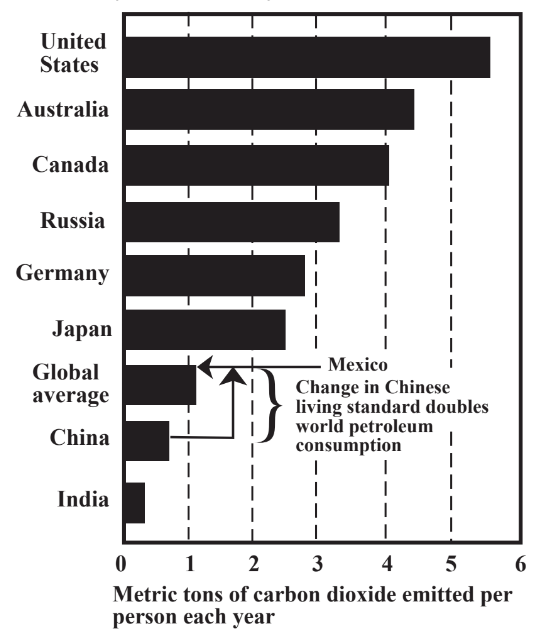
Reduction of demand per person for materials, energy, and other natural capital supplied by Earth through the application of sustainability science and technology must be accomplished to help mitigate the demands of high population. The second factor in the above equation, demand per person, may prove to be more intractable. A reasonable indicator of demand is reflected in the amount of carbon emitted per person each year, which reflects fossil fuel consumption as shown for several major countries in Figure 17.1. This figure shows that the more industrially developed countries emit the most per capita. However, the two countries with the largest populations, Chinaand India, have much lower carbon emissions per person. As the economies of these two giants grow, demand for material goods and energy-consuming services will grow as well. For example,if the average living standard of the citizens of China were to reach the modest level of those of Mexico, world petroleum consumption would have to double under conventional economic systems. Were the average person in China to live like the average person in the U.S., an impossible burden would be placed on Earth’s carrying capacity. Obviously, ways must be found to meet the basic resource demands per person in more developed countries and means found to deliver a high quality of life to residents of less developed countries without placing unsupportable demands on Earth’s resources.
Figure 17.1 illustrates another point regarding the relationship of population and consumption per capita, that the addition of population to more developed countries has a much greater impact on resources than it does on less developed nations. Taking per capita carbon emissions as a measure of impact, the addition of one person to the U.S. population has at least 10 times the impact as adding one person to India’s population. It may be inferred that immigration into the U.S. and other developed countries from less highly developed nations has an inordinate impact upon resources as the immigrants attain the living standards of their new countries.