Nuclear Kinetics (Worksheet)
- Page ID
- 16589
Name: ______________________________
Section: _____________________________
Student ID#:__________________________
Work in groups on these problems. You should try to answer the questions without referring to your textbook. If you get stuck, try asking another group for help.
Energetics of Nuclear Reactions (Einstein and Binding Energy)
In chemical reactions, matter undergoes a change in composition where atoms are rearranged. The Law of Conservation of Matter argues that both type and number of atoms are conserved in a normal chemical reaction. Since matter is conserved, then mass is conserved.
\[\underbrace{\text{Mass of Reactants } = \text{Mass of Products}}_{\text{chemical reactions}} \nonumber \]
However in nuclear reactions, matter undergoes a transformation where new matter is made. Atoms are not necessarily conserved, so mass is then not necessarily conserved.
\[\underbrace{\text{Mass of Reactants } \neq \text{Mass of Products}}_{\text{nuclear reactions}} \nonumber \]
Albert Einstein’s mass-energy equivalence relates energy and mass in nuclear reactions:
\[ E=mc^2 \label{Einstein} \]
Each time an energy change occurs, there is also a mass change that is related by the constant \(c^2\) (the speed of light squared). Compared to the amount of energy due to the nuclear reaction, energy changes in chemical reactions are small, making the mass change insignificant for chemical reactions. However, on a nuclear level, there is a significant amount of energy change in comparison and therefore a discernible mass change. In Albert Einstein’s mass-energy equivalence, we can rewrite Equation \(\ref{Einstein}\) to
\[\Delta E = \Delta m c^2 \label{E2} \]
where \(\Delta E\) is the energy difference after a net change of mass \(\Delta m\). For energy to be expressed in Joules, mass is expressed in kilograms and \(c\) in meters per second. Two units to express nuclear energy are joules (J) and megaelectronvolts (MeV).
\[1.6022 \times 10^{-13}\, J = 1\, MeV \nonumber \]
From Equation \(\ref{Einstein}\), the energy of 1 atomic mass unit (1 amu = \(1.66 \times 10^{-27}\, kg\)) is
\[\text{1 atomic mass unit (u) } = 1.4924 \times 10^{-10}\; J \nonumber \]
By knowing the mass change in amu, the energy released can be directly calculated using these conversion factors, which have already taken into account mass conversions and the value of \(c^2\). Keep in mind that the mass-energy sums of a nuclear reaction must equal each other (by the Laws of Conservation of Mass & Energy). The sum of the mass and energy of the reactants are equivalent to the sum of the mass and energy of the products. The Binding energy is the energy required to disassemble a whole system into separate parts. A bound system typically has a lower potential energy than the sum of its constituent parts; this is what keeps the system together. Often this means that energy is released upon the creation of a bound state (via Equation \(\ref{E2}\)).
Example \(\PageIndex{1}\): Binding energy of an Alpha Particle
Calculate the mass defect for the alpha particle (i.e., a Helium nucleus) \(^4_2He\) given the experimental mass of the alpha particle is \(4.0015\, amu\).
Solution
To solve this we need to add up the individual mass of the free nucleons that constitute the helium nucleus (alpha particle). We know that the mass of a neutrons is \(1.0087\, amu\) and mass of a proton is \(1.0073\, amu\).
The total mass of the free nucleons of a alpha particle is therefore
\[2 \times (1.00870\,amu) + 2 \times (1.0073\, amu) = 4.00320\, amu \nonumber \]
As expected, this is less than the alpha particle.
The difference in mass is therefore
\[\underbrace{4.0015\, amu}_{\text{mass of nucleus}} - \underbrace{4.0320\, amu}_{\text{mass of free nucleons}} = \,-0.0305\, amu \nonumber \]
The difference in mass can be converted to nuclear binding energy via Equation \(\ref{E2}\)
\[\begin{align*} E &= (-0.0305 \,amu) \left(\dfrac{1.6605 \times 10^{-27} kg}{1\, amu}\right) (3.00 \times 10^8 \,m/s)^2 \\[4pt] &= -4.55 \times 10^{-12} kg\, m^2/s^2 \\[4pt] &= -4.55 \times 10^{-12} J/nucleus \end{align*} \]
This does not seem like much energy (i.e., 4 trillionths of a joule), but remember this is for one alpha particle. 4.0026 grams of Helium nuclei (alpha particles) contains approximately \(6.022 \times 10^{23}\) nuclei, so
\[(-4.55 \times 10^{-12} J/ \cancel{nucleus}) (6.022 \times 10^{23} \cancel{nuclei}/mol = -2.74 \times 10^{12} J/mol \nonumber \]
That is over 2 trillion joules for just 4 grams of helium generated from free nucleons. That is a LOT of energy.
Q1
The masses of a free proton and a neutron are 1.007 825 amu and 1.008 665 amu.
- Calculate the binding energy for a \(\ce{^9Be}\) nucleus with a mass of 9.01219 amu.
- Calculate the binding energy for \(\ce{^37Cl}\) nucleus with a mass of 36.966 amu.
Q2
Why are there often many significant digits typically used for masses when discussing the binding energy of nuclei?
Q3
Which isotope has the highest nuclear binding energy per gram: 4He, 16O, 32S, 55Mn, 238U? (No calculation is necessary).
Nuclear Kinetics (Activity, Decay Kinetics, and Half Lives)
The rate of radioactive decay is an intrinsic property of each radioactive isotope that is independent of the chemical and physical form of the radioactive isotope. The rate is also independent of temperature. In this section, we will describe radioactive decay rates and how half-lives can be used to monitor radioactive decay processes. In any sample of a given radioactive substance, the number of atoms of the radioactive isotope must decrease with time as their nuclei decay to nuclei of a more stable isotope. Using N to represent the number of atoms of the radioactive isotope, we can define the rate of decay of the sample, which is also called its activity (\(A\)) as the decrease in the number of the radioisotope’s nuclei per unit time (note that activity is a rate):
\[A=-\dfrac{\Delta N}{\Delta t} \label{21.4.3} \]
Activity is usually measured in disintegrations per second (dps) or disintegrations per minute (dpm), although it used to be expressed in terms of Curies (\(1\, Ci = 3.70 \times 10^{10} s^{–1}\)). The activity of a sample is directly proportional to the number of atoms of the radioactive isotope in the sample:
\[A = kN \label{21.4.4} \]
Here, the symbol \(k\) is the radioactive decay constant, which has units of inverse time (e.g., s−1, yr−1) and a characteristic value for each radioactive isotope. If we combine Equation \(\ref{21.4.3}\) and Equation \(\ref{21.4.4}\), we obtain the relationship between the number of disintegrations per unit time and the number of atoms of the isotope in a sample:
\[-\dfrac{\Delta N}{\Delta t}=kN \label{21.4.5} \]
Equation \(\ref{21.4.5}\) is the same as the equation for the reaction rate of a first-order reaction, except that it uses numbers of atoms instead of concentrations. In fact, radioactive decay is a first-order process and can be described in terms of either the differential rate law (Equation \(\ref{21.4.5}\)) or the integrated rate law:
\[N = N_0e^{−kt} \nonumber \]
or
\[\ln \dfrac{N}{N_0}=-kt \label{21.4.6} \]
All spontaneous nuclear decay processes follow 1st order kinetics. This makes it convenient to discuss the kinetics in terms of half-lives and activity. For example, the half-life of 241Am is 432 years, \(1.364 \times 10^{10} s\). As with chemical kinetics, the relation between the rate constant and half-life of a 1st order reaction ( \(t_{1/2}= \ln 2/k\)), therefore the the rate constant for the decay of 241Am is \(k = 5.082 \times 10^{–11} s^{–1}\).
Because radioactive decay is a first-order process, the time required for half of the nuclei in any sample of a radioactive isotope to decay is a constant, called the half-life of the isotope. The half-life tells us how radioactive an isotope is (the number of decays per unit time); thus it is the most commonly cited property of any radioisotope. For a given number of atoms, isotopes with shorter half-lives decay more rapidly, undergoing a greater number of radioactive disintegrations per unit time than do isotopes with longer half-lives.
Q4
How long (in years) does it take for a sample of \(\ce{^{60}Co}\) (\(t_{1/2} = 5.271\; yr\)) to decay by 95.0%?
Q5
Radon, a radioactive noble gas, decays via a first order decay process. If its half-life is 4.0 days, how many grams of a 25-gram sample remain after 20.0 days have passed?
Q6
A sample of papyrus was analyzed using 14C dating to determine its age. The 14C activity is 2.15 dpm (disintegrations per minute). What is the approximate age of the papyrus in years given that the half-life of 14C is 5.73 x 103 years and the activity of 14C found in living materials is 12.6 dpm?
Q7
The data below was collected on the decay of an isotope. Determine the half-life of the isotope by graphical analysis. All important calculations must be shown on the graph!
| Day | Activity (cpm) |
Count time (minutes) |
log (Activity) |
|---|---|---|---|
| 0 | 7466 | 4 | |
| 2 | 6948 | 4 | |
| 4 | 6472 | 4 | |
| 6 | 5828 | 4 | |
| 8 | 4796 | 4 | |
| 10 | 4448 | 4 | |
| 12 | 4072 | 4 | |
| 14 | 3724 | 4 | |
| 16 | 3284 | 4 | |
| 18 | 3256 | 4 | |
| 20 | 2728 | 4 | |
| 22 | 2560 | 4 | |
| 24 | 2384 | 4 | |
| 26 | 2124 | 4 | |
| 28 | 2004 | 4 | |
| 30 | 1740 | 4 |
Fission (Induced Nuclear Reaction)
Nuclear fission is either a nuclear reaction or a radioactive decay process in which the nucleus of an atom splits into smaller parts (lighter nuclei). The fission process often produces free neutrons and gamma photons, and releases a very large amount of energy even by the energetic standards of radioactive decay. Fission is a form of nuclear transmutation because the resulting fragments are not the same element as the original atom. The two nuclei produced are most often of comparable but slightly different sizes, typically with a mass ratio of products of about 3 to 2, for common fissile isotopes. Most fissions are binary fissions (producing two charged fragments). It is an exothermic reaction which can release large amounts of energy both as electromagnetic radiation and as kinetic energy of the fragments (heating the bulk material where fission takes place). In order for fission to produce energy, the total binding energy of the resulting elements must be less negative (higher energy) than that of the starting element.
Fission is often initiated by a nuclear reaction of a high Z element with a free neutron. For example. fission can be initiated in a U-235 nucleus (a stable nucleus that does not undergo radioactivity) via bombardment with neutrons to generate K-92 and Ba-141 nuclei and three free neutrons (amoung other fission products).
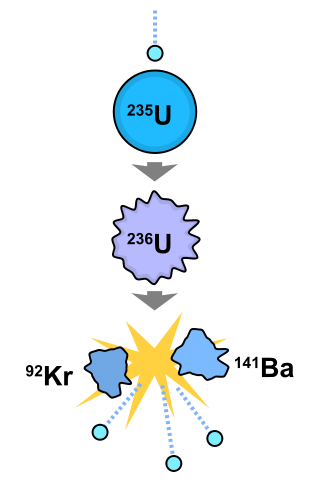
The nuclear reactions in Figure \(\PageIndex{2}\) can be written below:
\[ \underbrace{\ce{ ^1_0n + ^{235}_{92}U \rightarrow ^{236}_{92}U^*}}_{\text{step 1}} \nonumber \]
where \(\ce{^{236}_{92}U^*}\) is an excited and highly unstable nucleus that then decomposes into two nuclear and three neutrons
\[ \underbrace{\ce { ^{236}_{92}U^* \rightarrow ^{92}_{36}Kr + ^{141}_{56}Ba} + 3 ^1_0n}_{\text{step 2}} \nonumber \]
These daughter nuclei are also excited and relax via the emission of gamma rays or other emission processed (e.g., radioactivity).
Q8
Complete the following fission reactions:
- \(\ce{ ^{235}_{92}U + ^1_0n ⟶ ^{90}_{38}Sr\, + \,? \,+ 3 ^1_0n}\)
- \(\ce{_{92}^{235}U +^1_0n ⟶ _{43}^{107}Tc \,+ \,? \,+ 5 _0^1 n}\)
Q9
Given the following atomic masses: U-235: \(3.9029 \times 10^{-25} kg\), n: \(1.6749 \times 10^{-27} kg\), Xe-140: \(2.3234 \times 10^{-25} kg\), Sr-94: \(1.5595 \times 10^{-25} kg\). Determine the energy produced in the fission reaction below:
\[\ce{_{92}^{235}U + _0^1n ⟶ _{54}^{140}Xe + _{38}^{94}Sr} + 2 _0^1n \nonumber \]
Fusion (Induced Nuclear Reaction)
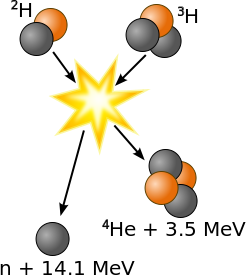
Nuclear fusion is a reaction in which two or more atomic nuclei come close enough to form one or more different atomic nuclei and subatomic particles (neutrons or protons). The difference in mass between the products and reactants is manifested as the release of large amounts of energy. This difference in mass arises due to the difference in atomic "binding energy" between the atomic nuclei before and after the reaction. Fusion is the process that powers active or "main sequence" stars, or other high magnitude stars. The easiest fusion reaction is:
\[ \ce{^2_1D + ^3_1T \rightarrow ^4_2He + ^1_0n} \nonumber \]
where \(T\) and \(D\) are the tritium and deuterium isotopes of hydrogen (Figure \(\PageIndex{3}\)). This reaction generates 14.1 MeV (via Equation \(\ref{E2}\)) and is common in research, industrial and military applications, usually as a convenient source of neutrons.
Q10
Calculate the energy released via the following fusion reaction
\[ \ce{2 ^2_1H \rightarrow ^4_2 He} \nonumber \]
The mass of deuterium is 2.014 amu and that of helium is given in Example \(\PageIndex{1}\).
Q11
Calculate the energy released via the following fusion reaction
\[ \ce{^7_3Li + ^1_1 H \rightarrow 2 ^4_2 He} \nonumber \]
the mass of lithium-7 is 7.016003 amu and the proton is given in Example \(\PageIndex{1}\).
Q12
Which reaction gives the most energy per mass: the fission reaction in Q9 or the fusion reaction in Q10?
Additional Questions
Q13
If the activity of \(\ce{^{111}Ag}\) were 2552 dps and after 120.5 minutes its activity had dropped to 1636 dps, what is the half-life of \(\ce{^{111}Ag}\) in minutes?
Q14
\(\ce{^{32}P}\) is used to treat some diseases of the bone. Its half-life is 14 days. Find the time it would take for a sample of \(\ce{^{32}P}\) to decay from an activity of 10,000 counts per minute to 8,500 counts per minute.
Q15
What would be the activity of the sample in question Q13 above after 24 days?
Q16
- A certain isotope has a half-life of 20 days. How long would it take for a sample of this isotope to decay from 10,000 cpm (counts per minute) to 4000 cpm?
- What would be the activity of the sample after 10 days?
Q17
Vanadium-49 has a half-life of 330 days. The initial activity of a 2-g sample of this isotope is 20000 counts per minute (cpm). How long will it take for the radiation of the isotope to go from 100 cpm to 50 cpm?
Q18
\(\ce{^{48}Cr}\) has a half-life of about 24 hours. If the initial activity of a sample of \(\ce{^{48}Cr}\) is 3000, what would the activity be after 60 hours?
Q19
\(\ce{^{131}I}\) transmutes to xenon during the decay process with a half-life of 8.02 days. How much \(Xe\) is produced after 400 grams of \(\ce{^{131}I}\) is allowed to decay for 24 days?
Q20
How much time would have to elapse before the radioactivity in a piece of wood, due to \(\ce{^{14}C}\) would drop from 14 counts per minute to 8 counts per minute (the half-life of \(\ce{^{14}C}\) is 5730 years).
Q21
- \(\ce{^{59}Fe}\) has a half-life of 45 days. If a steel piston ring had an initial activity of 10,000 counts per second what would the activity be after 100 days.
- How much time would have to elapse in order for the activity of the piston ring to drop from 10,000 counts per second to 4000 counts per second?
Q22
At one time on the Historic Tour in the Mammoth Cave park in Kentucky a mummified Native American, found in the caves was on display. Because of the cave conditions the Native American's body was well preserved. It was estimated that the Native American was about 145 pounds and died at the age of 45 from a falling rock that crushed his spinal column. Determine the approximate year of the Native American's death from the following data collected from the activity of \(\ce{^{14}C}\).
- Assume the initial activity of \(\ce{^{14}C}\) in his body was 15.7 cpm per gram of \(\ce{^{14}C}\).
- Current activity (circa 1950) ---11.76 cpm per gram of \(\ce{^{14}C}\).
- Halflife of \(\ce{^{14}C}\) is 5730 years.

