12: Calorimetry and Hess's Law (Experiment)
- Page ID
- 94000
- To experimentally measure the \( \Delta H\) values of two reactions using the technique of constant pressure calorimetry.
- To apply these \( \Delta H\) values in a Hess’s Law calculation to determine the enthalpy of combustion of a metal.
The combustion of a metal in oxygen produces the corresponding metal oxide as the only product. Such reactions are exothermic and release heat. For example, the combustion of iron releases 1651 kJ of heat energy for every four moles of iron burned:
\[ \ce{4Fe(s) + 3O2 (g) ->2Fe2O3 (s)} \quad \quad \Delta H_1 =-1651kJ \label{1}\]
Since it is difficult to measure the enthalpy of combustion of a metal directly, in this lab it will be determined indirectly by applying Hess’s Law of Heat Summation. Hess’s Law states that the enthalpy change of an overall process is equal to the sum of the enthalpy changes of its individual steps.
Determine \(\Delta H\) for the target reaction \( \ce{2 NO2 (g) + 1/2 O2 (g) -> N2O5 (g)}\) given the following information,
\[ \text{Reaction A } \quad \quad \ce{N2O5 (g) -> 2NO(g) + 3/2 O2 (g)} \quad \quad \Delta H_A =+223.7kJ \]
\[ \text{Reaction B} \quad \quad \quad \ce{NO2 (g) -> NO(g) + 1/2 O2 (g)} \quad \quad \Delta H_B =-57.1kJ \]
Solution
Reactions A and B have to be carefully manipulated before they can be summed to produce the target reaction. Reaction A must be reversed, causing a sign change to \( \Delta H_A\). Reaction B must be multiplied by a factor of 2, causing \( \Delta H_B\) to be multiplied by 2. Only then will they yield the target equation when added together:
\[ \ce{2NO(g) + 3/2 O2 (g) -> N2O5 (g)} \quad \quad \Delta H=−(+223.7)=-223.7kJ \]
\[+ \quad ( \ce{2NO2 (g) -> 2NO(g) + O2 (g)}) \quad\quad \Delta H=2 \times (-57.1)=-114.2kJ \]
\[ \ce{2NO2 (g) + 1/2 O2 (g) -> N2O5 (g)} \quad \quad \text{Target}\]
Thus, \(\Delta H_{\text{Target}} = -223.7 + (-114.2) = -337.9 kJ\)
In order to use Hess’s Law to find the heat of combustion of a metal, it is first necessary to obtain reaction enthalpies ( \( \Delta H\) values) for equations that can be summed together appropriately. To accomplish this, two reactions will be studied in this lab. In one reaction, a given metal will react with hydrochloric acid producing hydrogen and the metal chloride. In the other reaction, the corresponding metal oxide will react with hydrochloric acid producing water and the metal chloride. For example, the reactions involving iron and iron(III) oxide are as follows:
\[ \ce{2Fe(s) + 6HCl(aq) -> 2FeCl3 (aq) + 3H2 (g)} \quad \quad \Delta H_2 \label{2}\]
\[ \ce{Fe2O3 (s) + 6HCl(aq) -> 2FeCl3 (aq) + 3H2O(l)} \quad \quad \Delta H_3 \label{3}\]
Since both reactions are exothermic, the heat released (\(q\)) will be absorbed into the surrounding reaction mixture. As long as the reactions are performed in an insulated container (such as a coffee cup calorimeter) there will be negligible heat exchange with the container walls or outside air. By monitoring the temperature of the reaction mixture when specific quantities of reactants are used, the amount of heat (in J) released by these reactions can be determined by applying the equation:
\[ \text{heat released by reaction} (−q_{\text{reaction}}) = \text{heat absorbed by reaction mixture} (+q_{\text{mixture}}) = (m \times c \times \Delta T)_{\text{mixture}}\]
Here \(m\) is the total mass of the reaction mixture (in g), \( \Delta T\) is the maximum temperature change that occurs during the reaction (in °C), and \(c\) is the specific heat capacity of the mixture (in J/g°C). Note that since the reactions occur in aqueous solution, it is reasonable to substitute the specific heat capacity of water (= 4.184 J/g°C) for the specific heat capacity of the mixture.
Recall that at constant pressure (the conditions of this experiment), the heat released by the reaction equals the reaction enthalpy:
\[q_P = \Delta H\]
Since the heat released by each reaction is proportional to the amount of metal/metal oxide used, \(\Delta H_2\) and \( \Delta H_3\) can be easily calculated per gram or mole of metal/metal oxide used. It should be noted that reactions \ref{2} and \ref{3} by themselves still cannot be summed to produce Reaction \ref{1}. Another reaction is required:
\[ \ce{2H2 (g) + O2 (g) -> 2H2O(l)} \quad \quad \Delta H_4 \label{4}\]
\(\Delta H\) for this reaction (the formation of water from its elements) must be obtained from tabulated thermodynamic data in the textbook. Finally, the reactions \ref{2}, \ref{3} and \ref{4} and their enthalpies may be summed together according to Hess’s Law to determine the enthalpy of combustion of the given metal \ref{1}.
Procedure
Materials and Equipment
\(\ce{Mg}\) (s), \(\ce{MgO}\) (s), \(\ce{Zn}\) (s), \(\ce{ZnO}\) (s), \(\ce{Al}\) (s), \(\ce{Al2O3}\) (s), 1 M \(\ce{HCl}\) (aq), 6 M \(\ce{HCl}\) (aq), coffee cup calorimeter with lid*, thermometer*, looped stirring rod*, slotted stopper*, 100-mL graduated cylinder, 50-mL beaker, utility clamp, stand, electronic balance, and wash bottle.
*Items with an asterisk must be checked out from the stockroom.
Data Acquisition
Instead of a thermometer, some sections may use a data acquisition system (laptop computer, Vernier® interface, temperature probe, and LoggerPro® software) to directly monitor temperature changes over time. Detailed instructions for setting up this system will be provided at the beginning of your lab period. Please note that your experimental procedure will still be the same regardless of the method used to monitor temperature.
The Heat of Combustion of a Metal/Metal Oxide
- You will be assigned a specific metal/metal oxide pair to investigate by your instructor. Record their identities on your report form. Note that you will perform the following procedure for a total of four times, twice with the metal, then twice with the metal oxide.
- The table below indicates the quantities of reactants to be used for each metal/metal oxide combination. Note that the reactions involving \(\ce{Zn}\) and \(\ce{Al}\) require the concentrated 6 M acid.
|
\(\ce{Mg}\) / \(\ce{MgO}\) |
\(\ce{Zn}\) / \(\ce{ZnO}\) |
\(\ce{Al}\) / \(\ce{Al2O3}\) |
|---|---|---|
|
0.15 g \(\ce{Mg}\), 25 mL 1 M \(\ce{HCl}\) |
0.40 g \(\ce{Zn}\), 25 mL 6 M \(\ce{HCl}\) |
0.15 g \(\ce{Al}\), 25 mL 6 M \(\ce{HCl}\) |
| 0.25 g \(\ce{MgO}\), 25 mL 1 M \(\ce{HCl}\) | 0.60 g \(\ce{ZnO}\), 25 mL 6 M \(\ce{HCl}\) | 0.75 g \(\ce{Al2O3}\), 25 mL 6 M \(\ce{HCl}\) |
- Use an electronic balance to weigh your empty, dry calorimeter (the two nested Styrofoam® cups). Remove it from the balance, then pour approximately 25-mL of \(\ce{HCl}\) (aq) into it and weigh it again. Record these masses on your report (the difference is the mass of \(\ce{HCl}\) (aq) used).
- Now weigh an empty, dry 50-mL beaker. Remove it from the balance, then add the recommended mass of your assigned metal to it and weigh it again. Record these masses on your report (the difference is the mass of metal used).
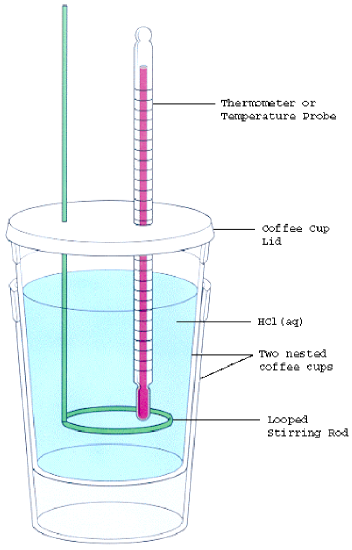
- Assemble your equipment as shown in the figure below. The thermometer (or temperature probe) and the stirring rod must be inserted through the holes in the calorimeter lid. The thermometer bulb should be immersed in the acid, but not touch the bottom of the calorimeter. Clamp the thermometer in place using the slotted stopper and utility clamp.
- Measure the temperature of the \(\ce{HCl}\) in the calorimeter (while covered with the lid). Once thermal equilibrium is established, record the temperature. Next, carefully add the metal sample to the acid. Quickly replace the lid and monitor the temperature change until the reaction is complete. Stir the mixture continuously with the stirring rod as the reaction occurs. Record the maximum temperature achieved by the mixture. Note that the mixture first warms up as the reaction occurs, but will then gradually cool as heat is lost to the surroundings. However, as Styrofoam is a poor conductor of heat this cooling will occur slowly. Thus it will be very easy for you to identify the maximum temperature.
- When finished, dispose of your chemical waste as directed by your instructor. Then rinse the calorimeter, thermometer and stirring rod thoroughly with distilled water, dry, and repeat the experiment again. Once you have completed both trials with the metal, perform your two trials using the metal oxide using the identical procedure.
Note that the thermometer must be clamped in place using the slotted stopper and utility clamp/stand. You may also want to place the nested cups in a medium beaker for extra stability.
Pre-laboratory Assignment: Calorimetry and Hess’s Law
- Show your work for all calculations. When 1.104 grams of iron metal are mixed with 26.023 grams of hydrochloric acid in a coffee cup calorimeter, the temperature rises from 25.2 °C to a maximum of 33.5 °C. The reaction that occurs is given below.
\[ \ce{2Fe(s) + 6 HCl(aq) -> 2FeCl3 (aq) + 3H2 (g)}\]
- Determine the amount of heat (in J) absorbed by the reaction mixture. Assume that the specific heat capacity of the mixture is the same as the specific heat capacity of water.
- How much heat (in J) was released by the reaction that occurred?
- Is this reaction exothermic or endothermic? Is \(\Delta H\) reaction positive or negative?
- Under constant pressure conditions (as used in this experiment), the heat released by the reaction equals the reaction enthalpy, \(q_{\text{released}} =\Delta H_{\text{reaction}}\). Determine \( \Delta H_{\text{reaction}}\) in Joules per gram of metal used (J/g).
- Determine \( \Delta H_{\text{reaction}}\) in kilojoules per mole of metal used (kJ/mol).
- Determine \( \Delta H_{\text{reaction}}\) in kilojoules for the balanced reaction equation provided (kJ).
- Consider the following three reactions:
\[ \ce{2Fe(s) + 6HCl(aq) -> 2FeCl3 (aq) + 3H2 (g)} \quad \quad \Delta H_A\]
\[ \ce{Fe2O3 (s) + 6HCl(aq) -> 2FeCl3 (aq) + 3H2O(l)} \quad \quad \Delta H_B\]
\[ \ce{2H2 (g) + O2 (g) -> 2H2O(l)} \quad \quad \Delta H_C\]
Show how these equations must be summed together according to Hess’s Law to determine \(\Delta H\) for the combustion of iron (target equation shown below). Also show clearly how the \( \Delta H\) values of each of the three reactions must be manipulated to determine the enthalpy of combustion of iron.
\[ \ce{4Fe(s) + 3O2 (g) -> 2Fe2O3 (s)} \quad \quad \Delta H=?\]
- Using tabulated \(\Delta H_f^o\) values in the text, determine the enthalpy change (in kJ) that occurs during the formation of water from its elements:
\[ \ce{2H2 (g) + O2 (g) -> 2H2O(l)} \quad \quad \Delta H=?\]
Note that this value (and the equation) will be used in your data analysis for this lab.
Lab Report: Calorimeter and Hess's Law
Metal + HCl Reaction
Experimental Data
Assigned Metal:
|
Trial 1 |
Trial 2 | |
|---|---|---|
|
Mass of dry, empty calorimeter |
||
|
Mass of calorimeter plus \(\ce{HCl}\) |
||
|
Mass of \(\ce{HCl}\) used |
||
|
Mass of dry, empty beaker |
||
|
Mass of beaker plus metal |
||
|
Mass of metal used |
||
|
Initial (equilibrium) temperature of \(\ce{HCl}\) |
||
|
Final (maximum) temperature of mixture |
Data Analysis
- Write the balanced equation for the reaction between your assigned metal and \(\ce{HCl}\). All balancing coefficients should be whole numbers.
- Complete the table below with the results of your calculations.
|
Trial 1 |
Trial 2 |
|
|---|---|---|
|
Total mass of mixture, \(m\) |
||
|
Temperature change of mixture, \(\Delta T\) |
||
|
SHC of mixture, \(c\) (use SHC of water) |
||
|
Heat absorbed by mixture, in J |
||
|
Heat released by reaction, in J |
||
|
\( \Delta H_{rxn}\) in J/g of metal used |
||
|
\( \Delta H_{rxn}\) in kJ/mol of metal used |
||
|
\( \Delta H_{rxn}\) in kJ for the rxn as balanced in \ref{1} |
||
|
Average \( \Delta H_{rxn}\) in kJ |
||
- Show your work for the following calculations using your Trial 1 data only:
- Heat absorbed by mixture, in J
- Heat released by reaction, in J
- \(\Delta H_{rxn}\) in J/g of metal used
- \( \Delta H_{rxn}\) in kJ/mol of metal used
- \( \Delta H_{rxn}\) in kJ for reaction as balanced in \ref{1}
- Is this reaction exothermic or endothermic? What is your experimental evidence supporting this? Is \(\Delta H_{rxn}\) positive or negative?
Metal Oxide + HCl Reaction
Experimental Data
Assigned Metal Oxide:
|
Trial 1 |
Trial 2 | |
|---|---|---|
|
Mass of dry, empty calorimeter |
||
|
Mass of calorimeter plus \(\ce{HCl}\) |
||
|
Mass of \(\ce{HCl}\) used |
||
|
Mass of dry, empty beaker |
||
|
Mass of beaker plus metal oxide |
||
|
Mass of metal oxide used |
||
|
Initial (equilibrium) temperature of \(\ce{HCl}\) |
||
|
Final (maximum) temperature of mixture |
Data Analysis
- Write the balanced equation for the reaction between your assigned metal oxide and \(\ce{HCl}\). All balancing coefficients should be whole numbers.
- Complete the table below with the results of your calculations.
|
Trial 1 |
Trial 2 |
|
|---|---|---|
|
Total mass of mixture, \(m\) |
||
|
Temperature change of mixture, \(\Delta T\) |
||
|
SHC of mixture, \(c\) (use SHC of water) |
||
|
Heat absorbed by mixture, in J |
||
|
Heat released by reaction, in J |
||
|
\( \Delta H_{rxn}\) in J/g of metal used |
||
|
\( \Delta H_{rxn}\) in kJ/mol of metal used |
||
|
\(\Delta H_{rxn}\) in kJ for the rxn as balanced in \ref{1} |
||
|
Average \(\Delta H_{rxn}\) in kJ |
||
Note: You are not required to show your work for the calculations you performed to complete the above table.
Enthalpy of Combustion of a Metal
- Write the balanced equation for the combustion of your assigned metal. All balancing coefficients should be whole numbers.
- Using Hess’s Law, determine the enthalpy of combustion of your assigned metal as balanced above. To do this, you will need the balanced thermochemical equations for the two reactions studied in this lab, plus the balanced thermochemical equation for the formation of water from its elements. Clearly show how these three equations (and their reaction enthalpies) must be combined to give the target combustion reaction.
- Calculate the theoretical value for the enthalpy of combustion of your assigned metal, using the tabulated \( \Delta H_f^o\) values from the text.
- Determine the percent error in your experimentally determined value for the enthalpy of combustion.