11A: The Molecular Weight of Carbon Dioxide (Experiment)
- Page ID
- 94002
- To determine the molecular weight (molar mass) of carbon dioxide based on measurements of the pressure, temperature, volume and mass of a sample of the gas.
- To compare the experimental molecular weight to the theoretical molecular weight of carbon dioxide.
From the ideal gas law, \(PV=nRT\), it is easy to show that the density of an ideal gas is:
\[D_{gas} = \dfrac{m}{V} = \dfrac{PM_w}{RT} \label{1}\]
where \(M_w\) is the molecular weight (molar mass) of the gas.
This can be solved to obtain:
\[M_w = \dfrac{mRT}{PV} \label{2}\]
Thus, the molecular weight (or molar mass) of a gas can be determined by measuring the temperature, pressure, volume and the mass of a sample of the gas.
In this experiment the molecular weight of carbon dioxide will be determined. The carbon dioxide gas is produced by the reaction of calcium carbonate with hydrochloric acid.
\[\ce{CaCO3 (s) + 2 HCl (aq) -> CO2 (g) + CaCl2 (aq) + H2O (l)} \label{3}\]
The carbon dioxide gas will be collected in an Erlenmeyer flask that is covered with aluminum foil. The foil and the fact that carbon dioxide gas is denser than air inhibit the rate at which the carbon dioxide mixes with the outside air.
The temperature of the gas will be measured by briefly placing a thermometer underneath the foil.
Since the flask is not sealed the pressure of the gas in the flask will be equal to the pressure in the laboratory. The laboratory pressure will be measured with a mercury barometer.
The volume of the gas is equal to the volume of the flask. The volume of the flask will be measured by filling it to the brim with deionized water. From the measured mass of the water and the known density of water the volume of the water, and thus the volume of the flask, will be determined. A table of densities of water at various temperatures is given below.
|
|
|
|---|---|
|
15 |
0.9991 |
|
16 |
0.9989 |
|
17 |
0.9988 |
|
18 |
0.9986 |
|
19 |
0.9984 |
|
20 |
0.9982 |
|
21 |
0.9980 |
|
22 |
0.9978 |
|
23 |
0.9975 |
|
24 |
0.9973 |
|
25 |
0.9970 |
|
26 |
0.9968 |
|
30 |
0.9957 |
Information from the CRC Handbook of Chemistry and Physics, 64th ed., 1983-4
The mass of gas in the flask can be determined by weighing the gas filled flask and then subtracting the mass of the empty flask. In most experiments the mass of an “empty” container is actually the mass of the container plus the air it holds. This is generally not a problem since the mass of the air is relatively small compared to the mass of a liquid or solid sample and can therefore be neglected. However when weighing a gas, not accounting for the mass of the air in the container would be a serious systematic error. The mass of air in the flask will be estimated from the volume of the flask and the known density of dry air. A table of dry air densities is given below. It is reasonable to approximate the air as being dry since the mole fraction of water vapor in air is very small (even in air that is saturated with water vapor the mole fraction of water vapor is only 0.03). The mass of the empty flask will then be calculated by subtracting the calculated mass of dry air from the measured mass of the flask filled with air. After the flask has been filled with carbon dioxide, it will be weighed, and the mass of the gas will be determined by subtracting the calculated mass of the truly empty flask.
Density of Dry Air
| Temperature (°C) | Density (g/L) | ||
|---|---|---|---|
| -- |
P = 750 torr. |
P = 760 torr. |
P = 770 torr. |
|
17 |
1.201 |
1.217 |
1.233 |
|
18 |
1.197 |
1.213 |
1.229 |
|
19 |
1.193 |
1.209 |
1.225 |
|
20 |
1.189 |
1.205 |
1.221 |
|
21 |
1.185 |
1.201 |
1.216 |
|
22 |
1.181 |
1.197 |
1.212 |
|
23 |
1.177 |
1.193 |
1.208 |
|
24 |
1.173 |
1.189 |
1.204 |
|
25 |
1.169 |
1.185 |
1.200 |
Information from the CRC Handbook of Chemistry and Physics, 64th ed., 1983-4
Procedure
Materials and Equipment
The following items must be obtained from the stockroom.
- A straight piece of glass tubing connected to a piece of rubber tubing
- A two holed rubber stopper with a thistle tube inserted into one hole and a piece of bent glass tubing (connected to a piece of rubber tubing) inserted into the other hole
- A \(\ce{CaCl2}\) drying tube
- A piece of aluminum foil that is approximately 15 cm by 15 cm and two 250-mL Erlenmeyer flasks are also needed. Make sure that the rubber stoppers will fit tightly into the mouth of each Erlenmeyer flask.
6 M hydrochloric acid is capable of causing serious chemical burns and blindness and should be handled with care. If the acid comes in contact with your skin immediately rinse the affected area with water for several minutes. As always, you should be wearing your safety goggles.
- Obtain one of the 250 mL Erlenmeyer flasks. This will be designated as flask B. Make sure that the flask is both clean and dry. Record the mass of the flask and the foil to the nearest 0.001 g using the analytical balance. Note that it is mass (flask + foil + air) that is being measured here. Also record the temperature of the air in the flask.
- Place about 25 grams of calcium carbonate into the other 250 mL Erlenmeyer flask designated as flask A. Add about 10 mL of water, or enough to cover the chips completely. Insert the two-holed rubber stopper (with the thistle tube and the bent tube) into flask A, making sure that the thistle tube is adjusted so that it is beneath the water but not touching the bottom of flask. The stopper must fit tightly into the flask. Also obtain about 25 mL of dilute (6 M) hydrochloric acid, \(\ce{HCl}\), in a small, labeled beaker.
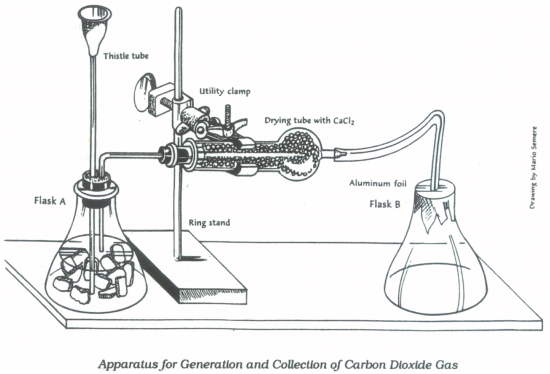
- Assemble the apparatus shown in figure 1. Insert the straight glass tube (the one that is attached to the flexible tubing but not attached to the one-holed rubber stopper) into flask B by placing it between the foil and the flask and pressing the foil against it to hold it in place. Be careful to fold and shape the foil only as much as necessary since it is fragile and will easily tear. Attach the flexible end of the tubing to the drying tube. The small rubber stopper attached to the bent glass tubing should be inserted into the other end of the drying tube.
- When all is ready pour 5–10 mL of the hydrochloric acid into the top of the thistle tube and allow it to run through the tube and into flask A. The reaction should begin immediately as evidenced by gas evolution. Allow the reaction to continue for at least 20 minutes to displace all of the air in flask B with carbon dioxide gas. During this time pay attention to what is happening in flask A; if the gas evolution ceases, add additional \(\ce{HCl}\) solution through the thistle tube. After the 20 minutes remove the tube from flask B (keep the foil in place) and immediately weigh the flask containing carbon dioxide on the analytical balance to the nearest 0.001 g.
- Reassemble the apparatus and allow gas evolution to continue and flow into flask B for an additional 15 minutes. Again, weigh flask B (with the foil). The two masses (before and after the 15 minutes) should agree closely (to within 0.005 g). If the mass has increased by more than 0.005 g reassemble the apparatus and continue to collect carbon dioxide gas for an additional 5 minutes then reweigh the flask. Continue this procedure until successive masses agree to within 0.005 g (or until a decrease in mass is observed). Next, measure and record the temperature of the carbon dioxide in the flask. Use the barometer to read the atmospheric pressure.
- Finally, in order to determine the volume of flask B, fill this flask with deionized water to the brim, wipe any water from the outside of the flask and weigh it, with the foil, to the nearest 0.01 g using the triple beam balance. Next, measure and record the temperature of the water. The volume of water in the flask can now be calculated from the mass and density of water in the flask at the temperature recorded.
Cleanup
Neutralize the contents of flask A and any unused \(\ce{HCl}\) by adding solid sodium bicarbonate until the solution no longer fizzes upon addition of additional bicarbonate. Remember that goggles should be worn at all times in the laboratory. This step is best performed in the sink as the flask tends to overflow. Decant off the liquid, leaving any solid marble chips behind. Rinse the chips with water and decant off the water. Pour the chips into the labeled recovery beaker.
Pre-laboratory Assignment: Molecular Weight of a Gas
- Write a balanced equation including state symbols for the reaction that takes place in flask A.
- A flask holds a total of 402.5 g of water at 20.4oC. What is the volume of the flask?
- Assuming that the pressure is 758.4 torr and the temperature is 24.6oC, calculate the mass of dry air in the flask.
- Assuming the mass of the flask filled with dry air is 125.383 g, calculate the mass of the empty flask.
- Assuming the mass of the flask filled with \(\ce{CO2}\) is 125.557g , the temperature is 23.2oC, and the pressure is 758.4 torr, calculate the molecular weight of \(\ce{CO2}\).
- Calculate the actual molecular weight of \(\ce{CO2}\) and determine the percent error.
Lab Report: Molecular Weight of a Gas
Data and Observations
| Mass of foil and flask filled with air | g |
|---|---|
| Temperature of dry air in flask | °C |
| Barometric pressure | mm Hg (torr) = atm |
| Density of dry air at experimental temperature and pressure | g/L = g/mL |
| Mass of foil and flask filled with \(\ce{CO2}\), after first twenty minutes | g |
| Mass of foil and flask filled with \(\ce{CO2}\), after second fifteen minutes | g |
| Mass of foil and flask filled with \(\ce{CO2}\), after additional five min (if needed) | g |
| Temperature of \(\ce{CO2}\) in flask | °C = K |
| Mass of flask filled with water | g (with foil) |
| Temperature of water | °C |
| Density of water at above temperature | g/mL |
Calculations and Analysis
- The volume of the flask is equal to the volume of water in the flask. This volume is calculated from the mass and the density of the water. The mass of the water is the difference between the mass(flask + foil + water) and the mass(empty flask + foil). However, since the mass of the water is much larger than the mass of air displaced by the water the mass of water can be approximated as the difference between the mass(flask + foil + water) (#9 on Data Sheet) and the mass(flask + foil + air) (#1 on Data Sheet). The density of water at different temperatures is tabulated above.
- The mass of dry air in the flask is calculated from the volume of the flask and the density of dry air at the recorded temperature and pressure. The density of dry air at different combinations of temperature and pressure is tabulated above.
- The mass of the empty flask is equal to the difference between the mass(flask + foil + air) (#1 on Data Sheet) and the calculated mass of dry air.
- The mass of carbon dioxide in the flask is determined by subtracting the mass of the empty flask from the largest value of mass(flask + foil + carbon dioxide) (the largest value of #6 or #7 on the Data Sheet).
- The molecular weight of carbon dioxide is calculated using Equation \ref{2}.
- The percentage error can be calculated using the following formula.
\[\text{Percentage Error} = \frac{|(\text{Experimental Value}) – (\text{Theoretical Value})|}{(\text{Theoretical Value})} \times 100 \]
For each calculation, show your work and put a box around each answer.
- Volume of flask
- Mass of dry air in flask
- Mass of empty flask
- Mass of carbon dioxide in flask
- Experimental molecular weight
- Percentage Error
Questions and Conclusions
- Because the mass of the flask with water exceeds the amount that can be weighed on the digital balances, the triple-beam-balance is used, which only weighs to ±0.01 g. Why doesn't using this balance affect the number of significant digits to which the experimental molecular weight of carbon dioxide can be reported?
- Why can we neglect the mass of the air in the flask when obtaining the mass of the water in the flask (as we do when weighing most things) but not neglect the mass of the air when we calculate the mass of carbon dioxide in the flask?
- Suggest a possible source of error that would account for any discrepancy between your experimentally determined molecular weight and the theoretical molecular weight.