13: Nuclear Weapons
- Page ID
- 19588
The First Atomic Bombs
Destined for use in the first atomic bombs, fissionable materials — solid uranium tetrafluoride from Oak Ridge, Tennessee, and plutonium nitrate paste from Hanford, Washington — began to arrive at the secret laboratory in Los Alamos, New Mexico in late 1944 (Figure \(\PageIndex{1}\)). On the lava flows of an extinct volcano 35 miles north of Santa Fe, Robert Oppenheimer, a brilliant physicist from the University of California, led the development of the first nuclear fission weapons. Chemists purified the two metals and metallurgists shaped them into forms suitable for the weapons. Plutonium presented unique problems because it had never been isolated in large amounts and because the solid had six separate phases.
At first glance, making a fission bomb is simple: assemble a supercritical mass of fissile material, and a chain reaction will rapidly produce neutrons that, in turn, generate more fission and neutrons. The challenge is to bring two subcritical masses together quickly before the energy released by the initial fission blows the masses apart and stops the chain reaction.
The physicists had to answer two fundamental questions: how much fissile material would be required for the weapons, and how much time would be needed for an effective detonation. The initial calculations for the mass of U-235 required for a bomb looked like this:
They wanted a 20-kiloton explosion (equivalent to 20,000 tons of TNT), so
\[ 20 \text{ kilotons TNT} = 1 \times 10^{13} cal = 8.4 \times 10^{13} joules \nonumber \]
If each fission produces \(3.2 \times 10^{-11} joules\), then the number of fissions events (\(N\)) required is
\[ N = \dfrac{8.4 \times 10^{13} joules}{3.2 \times 10^{-11} joules / \text{fission event}} = 2.6 \times 10^{24} \text{fission events} \nonumber \]
Thus, the mass of U-235 required would be
\[ moles_{235} = 2.6 \times 10^{24} \text{atoms} \left(\dfrac{1 \text{ mole } \text{U-235}}{6.02 \times 10^{23} \text{atoms}} \right) \nonumber \]
The physicists calculated a 10% efficiency for the weapon so
\[m_{235} = 4.3 \, moles ( 235 \, g/mole) \times 0.10 = 10 \, kg \nonumber \]
The time required for an effective detonation can be calculated from the basic exponential equation for neutron production.
\[N_n = N_o e^{(k-1)n} \nonumber \]
If \(N_o = 1\) and \(k-1 = 0.693\), then
\[N_n = N_o e^{(0.693)n} = 2^n \label{eq1} \]
One might expect that \(k\), the number of neutrons produced per fission, would be larger. However, neutron absorption by U-238 and leakage of neutrons from the supercritical mass reduce the number of neutrons available to sustain the chain reaction.
This exponential equation generates the following data (Table \(\PageIndex{1}\)). Remember that the total number of neutrons produced at the time of a particular generation is the sum of all of the neutrons from all generations. Thus, in the 4th generation (n = 3), 15 neutrons have been produced.
| n (generation) |
N (# of fissions per generation) |
Total # neutrons produced | n (generation) |
N (# of fissions per generation) |
Total # neutrons produced |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 10 | 1024 | 1.28 x 103 |
| 2 | 2 | 3 | 20 | 1.05 x 106 | 1.05 x 106 |
| 3 | 4 | 7 | 30 | 1.07 x 109 | 1.07 x 109 |
| 4 | 8 | 15 | 40 | 1.10 x 1012 | 1.10 x 1012 |
| 5 | 16 | 31 | 50 | 1.13 x 1015 | 1.13 x 1015 |
| 6 | 32 | 63 | 60 | 1.15 x 1018 | 1.15 x 1018 |
| 7 | 64 | 127 | 70 | 1.18 x 1021 | 1.18 x 1021 |
| 8 | 128 | 255 | 80 | 1.24 x 1027 | 1.24 x 1024 |
The time required is calculated as follows. First, calculate the number of generations by substituting the number of fissions required to produce the equivalent of 20 kilotons of TNT into Equation \ref{eq1}:
\[ \left(\dfrac{1}{2} \right) 2.6 \times 10^{24} = 2^n \nonumber \]
\[\ln (1.34 \times 10^{24}) = n\,\ln 2 \nonumber \]
\[n = 80\, generations \nonumber \]
Next calculate the time period for one generation, which is the time required for a neutron to travel across the diameter of the critical mass. We need to calculate the diameter of the critical mass assuming a sphere.
\[\rho = \dfrac{mass}{volume} \nonumber \]
The
\[volume = \dfrac{4}{3} \pi r^3 \nonumber \]
so
\[r = \left(\dfrac{3m}{4\pi \rho}\right)^{1/3} = 0.05\,m \nonumber \]
where \(\rho\) is the density of uranium ( \(1.87 \times 10^4 \,kg/m^3\))
Physicists experimentally determined the velocity (\(v\)) of neutrons to be \(1 \times 10^7 \,m/sec\), so the time (\(t\)) required for a single generation is
\[t = \dfrac{2r}{v} = \dfrac{0.1\,m}{1 \times 10^7} = 10^{-8} \,\text{sec for one generation} \nonumber \]
Thus, the time for 80 generations is approximately \(80 \times 10^{-8} sec\) or 1 microsecond. The exponential growth of neutrons means that the last 10 generations produce approximately 99.9% of the energy in the explosion. Thus, it is important to keep the supercritical mass together long enough to release the desired amount of energy.
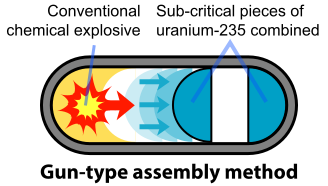
To prevent spontaneous detonation of an atomic bomb, the fissile material is kept in a subcritical configuration. It is then rapidly assembled into a supercritical mass using conventional explosives. Once the bomb has achieved this mass, any neutron introduced into it will be likely to initiate a chain reaction. The mechanism for "Little Boy", the U-235 bomb, was a gun that fired one subcritical piece of U-235 into another to form a supercritical mass (Figure \(\PageIndex{2}\)). The pieces had to be assembled within a time less than the average time between appearances of spontaneous neutrons from either U-235 or cosmic radiation. A conventional explosive in an artillery barrel could fire the U-235 mass at speeds of a few millimeters per second, fast enough to prevent a fizzle caused by a spontaneous neutron setting off a premature chain reaction.
Originally, the gun-type mechanism was planned for both the U-235 and Pu-239 weapons. However, a problem arose with the Pu-239 bomb that required a different assembly mechanism because of the small amount of Pu-240 that is produced with the Pu-239 in the reactor.
Pu-240 emits large numbers of neutrons spontaneously: 1,030 neutrons per gram per second compared with 0.0004 neutrons per gram per second for U-235. Even at a concentration of 1% Pu-240 in the fissile Pu-239, the required mass of Pu emits 52,000 neutrons per second or one neutron every 20 microseconds. Thus, it is very probable that a neutron from Pu-240 will initiate a premature chain reaction during the critical last 100 microseconds of the critical mass in a gun-type assembly. This problem was discovered in mid 1944, well after the start of construction of the massive Hanford plutonium production facilities.
Removal of the Pu-240 was impractical. So the scientists and engineers looked for a faster method of assembling the plutonium. A mechanism based on implosion provided the solution to this problem. In this design, the fissile material is shaped into a single sphere with a mass slightly less than critical (Figure \(\PageIndex{3}\)). Layers of carefully shaped high explosives surround the sphere. When the explosives are detonated, the force of the shock wave compresses the fissile material into a smaller volume, forming a supercritical mass. This method of assembly is much faster than the gun-type mechanism and thus eliminates the problems resulting from spontaneous neutron emission of Pu-240. The spherical mass resulted in a pumpkin-shaped weapon called "Fat Man".
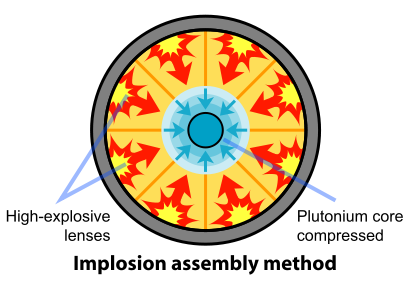
Figure \(\PageIndex{3}\): Fat Man: Implosion-type bomb. (Public Domain).
To assure that a chain reaction occurs, an initiator is placed at the center of the sphere of fissile materials. It consists of polonium, a source of alpha particles, and beryllium surrounded with thin gold foil. When the initial explosion squeezes the fissile material into a supercritical mass, the foil breaks, allowing the alpha particles to reach the beryllium and produce the initial neutrons according to the following reaction:
\[ \ce{^{4}_2He + ^{9}_4Be -> ^{12}_6C + ^{1}_0 n} \nonumber \]
Placing a neutron-reflecting material around the fissile material reduces the amount of Pu-239 or U-235 required to achieve a critical mass. This material increases the efficiency of the weapon in two ways: It reduces the loss of neutrons by leakage by reflecting them back into the supercritical mass, and it serves as material against which the expanding fission reaction can push. This latter function became known as "tamping" and increased the period of time before the weapon blew itself apart. Beryllium was often used as a tamper material.
In July 1945, the United States had enough fissile material for one uranium and two plutonium weapons. The scientists and engineers felt confident that the gun-type assembly mechanism for Little Boy would function properly. Besides, they did not have the material for a test device. They were less confident about the implosion mechanism on the plutonium weapon and felt that a test was necessary. On July 16, 1945, the first nuclear device, known as "The Gadget", was placed on a 100-foot tower and successfully detonated in the Alamogordo Desert, 200 miles south of Los Alamos (Figure \(\PageIndex{4}\)).

As the war with Japan continued and a costly allied invasion loomed as a real possibility, President Truman approved the use of nuclear weapons against selected Japanese targets. The U.S. Army Air Force received orders to use these weapons anytime after August 3, 1945. On August 6, "Little Boy" was dropped on Hiroshima (Figure \(\PageIndex{5}\)).

Little Boy was a uranium weapon containing 141.4 pounds of fissionable material containing 82.7% U-235. Only about two pounds fissioned, releasing an energy equivalent to 15-16,000 tons of TNT. The immediate effects of the blast killed an estimated 70,000 people, and by the end of 1945 an additional 20,000 to 70,000 deaths occurred, many due to lack of adequate medical resources.
Three days later, "Fat Man" destroyed a large part of Nagasaki (Figure \(\PageIndex{6}\)). Fat Man contained 13.6 pounds of Pu-239, of which only 2 pounds underwent fission. The explosive yield was equivalent to about 22,000 tons of TNT. The weapon caused from 40,000 to 75,000 immediate deaths with an estimated 80,000 deaths by the end of 1945. The weapons detonated at an altitude of between 1650 and 1900 feet, which maximized the blast effects but caused little long term radioactivity.

Figure \(\PageIndex{6}\): Fat Man – Detonated over Nagasaki Japan - Aug 9, 1945. Courtesy of the U.S. Department of Defense
The Development of Nuclear Weapons after World War II
The use of nuclear weapons by the United States to hasten the end of the war initiated a nuclear arms race between the United States and the Soviet Union that lasted until the end of the Cold War in 1992. During this period, scientists in both countries developed powerful thermonuclear fusion weapons (hydrogen bombs) and as well as more efficient fission bombs. Table \(\PageIndex{2}\) compares the explosive power of current nuclear warheads. A nuclear weapon includes the warhead encased in a bomb or missile.
| Terrorist weapon (improvised nuclear device) | < 3 kilotons |
| Bunker buster or tactical nuclear weapon | 3 to 5 kilotons |
| Fission weapon (Pu-239 or U-235) | 15 to 50 kilotons |
| Boosted fission weapon | 100 to 500 kilotons |
| Thermonuclear weapon | 1 to 57 megatons |
Improvised nuclear devices (IND) are low yield weapons that might be assembled by non-state groups or “rogue” nations for a terrorist attack. The most likely scenario would be the acquisition of a critical mass of HEU and construction of a simple gun-type assembly mechanism. The unit on proliferation provides more information.
Tactical nuclear warheads are placed in a variety of delivery systems such as artillery shells, torpedoes, cruise missiles, and bombs. These weapons may be defined by their range, which is usually shorter than that of strategic weapons, their targets, which are commonly battlefields or theaters of war, their yields, which are generally less than those of strategic weapons, and what organization controls the weapons. Bunker busters are designed to deliver nuclear warheads to hardened, underground targets.
Nuclear weapons with yields greater than 5 kilotons of TNT are known as strategic weapons. They are designed to be used on targets such as missile launch sites, command and control centers, large cities, or industrial sites. The two types of early fission weapons have been discussed in the previous sections. Boosted warheads contain a small amount of deuterium and tritium (isotopes of hydrogen) gases, which undergo fusion with the initiation of the fission reaction.
\[\ce{^{2}_1H + ^{3}_1H -> ^{4}_2He + ^{1}_1n} + \text{energy} \nonumber \]
The fusion releases an intense burst of high energy neutrons which amplifies the fission chain reaction, along with a small amount of energy This boosting allows increased yields from smaller, lighter warheads. Most current fission weapons contain boosted warheads. The 12 year half-life of tritium requires that these warheads be replenished at regular intervals.
Finally thermonuclear warheads, developed during the Cold War, use a series of fission-fusion-fission reactions to produce yields several orders of magnitude greater than those of fission devices (Figure \(\PageIndex{7}\)). Weapons designers have also reduced the size of thermonuclear warheads so that multiple warheads could be carried by a single missile. Today, a ballistic missile submarine can carry 24 missiles each with 6 thermonuclear warheads.
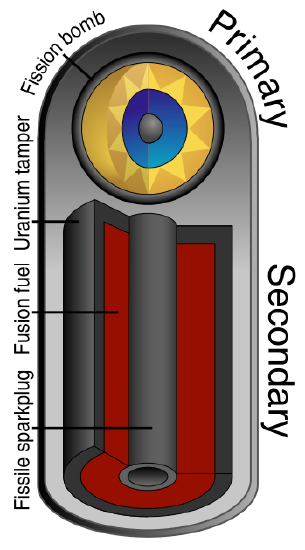
Initially the fission reaction of the primary releases gamma and X-radiation, neutrons, and heat to produce the high temperatures required for following the fusion reactions. The fuel for the fusion is lithium deuteride, \(\ce{^6Li_3^2H_1}\). The neutrons react with lithium to produce tritium, \(\ce{^3H_1}\), and alpha radiation.
\[ \ce{^6Li_3} + \ce{^1n_0} →\ce{^3H_1} + \ce{^4He_2} \nonumber \]
At the high temperature created by fission of the primary, the tritium then undergoes fusion with the deuterium in the lithium deuteride fuel.
\[ \ce{^{3}_1H + ^{2}_1H → ^{4}_2He + ^{1}_0n} + \text{energy} \nonumber \]
The fusion reaction liberates a huge amount of energy and creates large numbers of high energy neutrons, which cause the additional fission of the uranium surrounding the secondary.
Complete Bibliography on Nuclear Weapons Design from the Alsos Digital Library for Nuclear Issues
Contributors
Frank A. Settle (Washington and Lee University)


