The Van Deemter equation
- Page ID
- 61067
Abstract
The efficiency of a column is measured by theoretical plates, Nth, and can be normalized with the length of the column to give the height equivalent theoretical plate, called HETP or H. The Van Deemter equation describes the various factors influencing H, and is divided into eddy diffusion, longitudinal diffusion, and mass transfer terms. The relative importance of these factors varies with mobile phase velocity. Particle size and morphology contribute to H, along with a variety of other factors. Understanding the van Deemter equation allows the determination of the optimum mobile phase velocity.
Keywords
Van Deemter equation, A term, B term, C term, Mobile phase velocity, Column, Particle size, Efficiency, Height equivalent theoretical plate, HETP (H), Eddy diffusion, Longitudinal diffusion, Mass transfer, Particle shape, Wall effect, Porosity, Diffusion coefficient, Retention factor, Viscosity, Temperature, Optimal flow
Level: Basic
The theoretical plate number Nth shows the relation between retention time and peak width and describes column quality and separation power.
Factors affecting column efficiency (plate number)
- Column length
- Particle size
- Packing quality
- Linear velocity (flow)
- Instrument quality (dead volume)
- Retention factor
Stationary phase particle size is one of the most important factors in the van Deemter equation. For a given column length, the plate number (Nth) is inversely related to the particle size of the column packing. The smaller the particles, the higher the plate number and the separation power.
The plate number is also dependent on the flow rate (F) of the mobile phase. There is a certain velocity, the so-called optimum flow, at which the plate number is highest (and H is lowest). A lower or a higher flow rate provides less plates (higher H). In routine HPLC, columns are always operated at velocities above the optimum. The reduced column efficiency is less significant than the shorter analysis time at the higher than optimal flow rates.
To describe the contribution of the above factors, several so-called plate height equations have been developed. A plate height equation expresses the correlation between plate height and mobile phase velocity. Best known is the van Deemter equation, which describes the various contributions to plate height (H). In this equation the parameters that influence the overall peak width are expressed in three terms:
\[H = A + \dfrac{B}{u} + C \times u\]
H = HETP (plate height)
A = eddy diffusion term
B = longitudinal diffusion term
u = linear velocity
C = Resistance to mass transfer coefficient
Peak height and peak broadening are governed by kinetic processes in the column such as molecular dispersion, diffusion and slow mass transfer. Identical molecules travel differently in the column due to probability processes. The three processes that contribute to peak broadening described in the van Deemter equation are:
- A-term: eddy diffusion: The column packing consists of particles with flow channels in between. Due to the difference in packing and particle shape, the speed of the mobile phase in the various flow channels differs and analyte molecules travel along different flow paths through the channnels.
- B-term: longitudinal diffusion: Molecules traverse the column under influence of the flowing mobile phase. Due to molecular diffusion, slight dispersions of the mean flow rate will be the result.
- C-term: resistance against mass transfer. A chromatographic system is in dynamic equilibrium. As the mobile phase is moving continuously, the system has to restore this equilibrium continuously. Since it takes some time to restore equilibrium (resistance to mass transfer), the concentration profiles of sample components between mobile and stationary phase are always slightly shifted. This results in additional peak broadening.
van Deemter H-u curve
The van Deemter equation is graphically expressed in the H-u curve, which is a plot of the plate height as a function of the mobile phase velocity.
The H-u curve shows that:
- The A-term is independent of u and does not contribute to the shape of the H-u curve..
- The contribution of the B-term is negligible at normal operating conditions. This is due to the fact that the molecular diffusion coefficient in a liquid medium is very small.
- The C- term increases linearily with mobile phase velocity and its contribution to the H-u curve is therefore considerable. A small C-term leads to a fairly flat ascending portion of the H-u curve at higher mobile phase velocities. This means that the separation can be carried out at higher mobile phase velocities without sacrificing separation quality.
van Deemter H/u curve
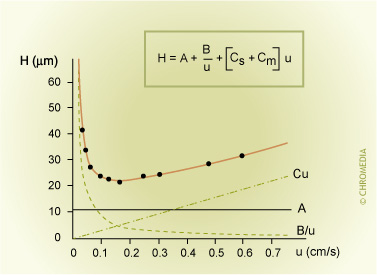
The H-u curve is very useful to determine the optimum mobile phase velocity uopt at which the highest column efficiency wil be attained. Below this velocity the column efficiency will decrease rapidly, whereas above the optimum velocity there is only a slight decrease in efficiency.
General rules of thumb:
- The smaller the plate height H, the more efficient the column. However, at the optimum flow rate (with the lowest H), the analysis time will in most cases be unacceptably long.
- Below the optimum flow rate the analysis time is too long and the quality of the separation suffers because of longitudinal diffusion (contribution of the B-term).
- At extremely high flows, both the separation quality and the pressure drop across the column will become unacceptable.
- The practical flow is often two or three times the optimum velocity. At these values, the minor loss of efficiency is still acceptable.
- Small particles (< 5 µm) allow an increase in the flow to reduce the analysis time without significantly lowering resolution between the peaks of interest.
Separation and (optimum) velocity
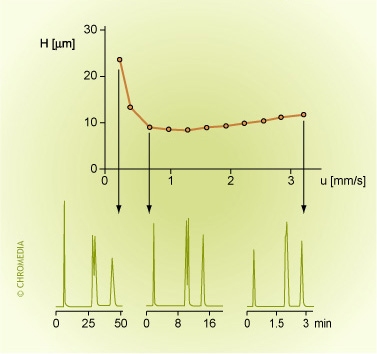
Eddy Diffusion (A-term)
The A-term in the Van Deemter equation describes the peak broadening due the presence of stationary phase particles in the column. In the literature it is called ' eddy diffusion'.
Eddy diffusion occurs as a result of multiple flow paths through a packed column bed. Analyte molecules cannot flow along a straight path through the column. Each analyte molecule follows a different flow path, which causes dispersion (differential path lengths). Some molecules will travel more slowly and will lag behind the zone (peak) centre, others will follow shorter paths and are slightly ahead. This effect results in slight differences in retention.
The homogeneity of the packed bed strongly affects the A-term. The probability of differential pathlengths due to radial movements is greater in a column having a poorly packed bed. Eddy diffusion is important for columns with internal diameters of 2 - 5 mm. However, when a column of this size is packed regularly with small, spherical particles with small dispersion in particle size, the contribution from eddy diffusion in the van Deemter equation will be a minimal.
CHROMEDIA PROGRAM
Eddy diffusion in the van Deemter equation is independent of the flow velocity of the mobile phase. In reality it appears that this is not entirely true, particularly at low flow rates. This can be seen in the above H-u curve.
Factors influencing A-term ('eddy' diffusion)
- Particle size dp
- Particle shape (regular or irregular?)
- Particle pore structure / shape
- Quality of the column packing
- Wall effects (material, roughness, column diameter)
Eddy diffusion is affected by the packing material in the column, specifically:
- Particle size: The larger the particles, the stronger the dispersion effect.
- Particle shape: For regularly shaped particles (spherical) the path length between the particles is smaller than for irregular particles. This is due to the fact that spherical particles can more easily form a regularly packed column bed. Conversely, an irregularly packed bed consists of flow channels of different shapes and diameters, resulting in different mobile phase velocities.
Longitudinal Diffusion (B-term)
The B-term in the van Deemter equation, also known as longitudinal diffusion, refers to the diffusion of individual analyte molecules in the mobile phase along the longitudinal direction of a column. Longitudinal diffusion contributes to peak broadening only at very low flow rates below the minimum (optimum) plate heigth.
Molecular diffusion takes place independent of the longitudinal (= axial) flow direction. Longitudinal diffusion is the result of concentration differences in the mobile phase. In the center of the peak zone the concentration is at its maximum. The concentration before and after the peak zone is lower. This results in diffusion, both in the direction of the mobile phase flow as well as in the opposite direction.
Some molecules move faster and others will move slower relative to the average velocity, resulting in peak broadening. This effect will be relatively great at long residence times in the column, which is the case at low flow rates. As the flow rate increases, this effect will contribute less to the total peak broadening. In practice, it is best to select flow rates that minimise the effect of longitudinal diffusion on column efficiency.
CHROMEDIA PROGRAM
Longitudinal diffusion is proportional to the molecular diffusion coefficient. It obeys Fick’s law and is therefore affected by viscosity, temperature and molecular size (~ weight). Increased temperature and diffusion coefficient increase the B term, while increased viscosity decreases it. Diffusion coefficients for components in liquids are generally very small. Because the mobile phase velocity is much higher than the diffusion coefficient of the component in solution, the B term is hardly significant in liquid chromatography and is typically neglected.
Influences on B-term (longitudnial diffusion):
- Linear velocity of the mobile phase
- Diffusion coefficient of analyte in the mobile phase Dm
- Mobile phase viscosity γ
- Temperature
- Type of analyte (molecular mass)
Mass Transfer (C-term)
The C-term in the van Deemter equation relates to the mass transfer of sample components between the stationary phase and the mobile phase during separation. The overall C-term is divided into two separate mass transfer terms:
- Cm-term, describing the contributions to peak broadening in the mobile phase. Because the linear velocity of the mobile phase is lower closer to the column wall (or the stationary phase particles) than in the center (or further away from the particles), the analyte molecules experience different velocities. This results in peak broadening in the mobile phase. This phenomenon is described by the Cm term.
- Cs-term, describing the contributions to peak broadening in the stationary phase. The Cs-term is determined by the amount of stationary phase (low is advantageous for the efficiency) and the extent of interaction of the sample on the phase (represented by the retention factor) and the distances the sample molecules have to travel.
Sample components (analytes) are retained in a chromatographic column due to their interaction with the stationary phase. Analyte molecules present in the flowing mobile phase diffuse towards the mobile/stationary pase interface, and enter into the stationary phase. To maintain partition equilibrium, some molecules will return to the mobile phase. After some time there will be a reverse process as the analytes move from the stationary phase into the mobile phase. This results in a continuous mass transfer taking place between the flowing mobile phase and the stagnant stationary phase during the course of the separation.
Resistance to mass transfer is dependent on the speed with which the partition equilibrium between mobile and stationary phase is obtained. Since the resistance to mass transfer in the mobile phase is not the same for all molecules of one type of analyte (it depends on the location in the column at a particular time and the distance they have to travel to partition between phases) this will also result in peak broadening of that analyte in the column.
Resistance against mass transfer in mobile phase
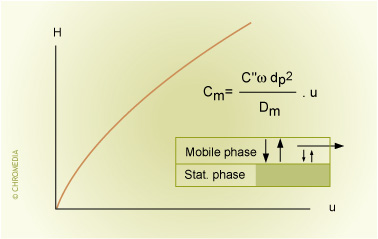
C" is a constant factor, related to the retention factor k of the peak of interest. Omega is related to the solvent volume of the column between and in the particles (pores), accessible for the mobile phase. Another important parameter affecting the Cm-term is particle diameter. Smaller particles will result in narrower flow channels and less contribution to mass transfer in the mobile phase.
Influences on Cm-term:
- Particle size dp
- Linear velocity u of the mobile phase
- Diffusion coefficient in the mobile phase
- Porosity of the packing particles
- Viscosity of the mobile phase
- Retention factor k
- Temperature
When analyte molecules can move quickly back and forth between mobile and stationary phase, the column efficiency is greatly improved. The speed with which analyte molecules move back and forth between phases is related to the diffusion coefficient of the analyte molecule in a particular mobile phase. Analyte molecules with large diffusion coefficients in the mobile phase will need less time to move to the mobile/stationary phase interface. The same applies for the movement into and out of the stationary phase. The viscosity and temperature also have an effect on diffusion.
Resistance Against Mass Transfer in Stationary Phase
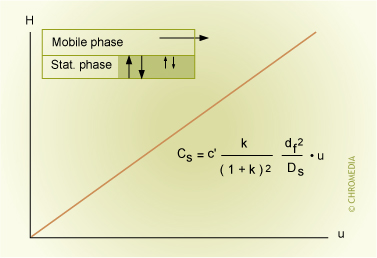
Equilibrium is reached faster with a larger molecular diffusion coefficient for the mobile phase and with a smaller particle diameter. This means that the contribution of the Cm and Cs to plate height decreases and the separation is more efficient. The contribution of the two C-terms to the overall peak broadening appears to increase with the linear velocity of the mobile phase. As mobile phase velocity increases, the exchange of molecules between mobile phase and stationary phase must be fast enough to keep up if the equilibrium between the phases is to be maintained. If equilibrium is not maintained, the peaks broaden and the efficiency and separation quality decrease.
Influences on Cs-term:
- Quality of stationary phase
- Diffusion coefficient in stationary phase
- Retention factor k
- Temperature
- Particle size
- Mobile phase velocity
The k value influences both C terms. The relative band broadening and thus the plate number appears to be dependent on the extent of interaction of a component with the stationary phase. Therefore, it becomes important to consider which peak is used to calculate a column's plate number. This dependence is strongest at the beginning of the chromatogram and decreases at higher retention factors. Thus Nth is the best calculated from a peak somewhere at the end of the chromatogram (k>5).

