Text
- Page ID
- 302684
1. Starting with 30 ml of a solution that is 0.1 M in butylamine, calculate the original pH, and then the pH as 5 ml increments of 0.1 M hydrochloric acid are added. Continue the series of calculations until 40 ml of acid have been added. Plot the data (pH on the y axis, volume of added acid on the x).
Has 99.9% of the butylamine been titrated at the equivalence point?
Butylamine is a base (Kb = 3.98\(\times\)10-4). Hydrochloric acid is a strong acid, so it will convert the butylamine into the butylammonium ion by a neutralization reaction. Remember, the Kn of a neutralization reaction will always be large if one of the species is strong.
Calculating the initial pH of a weak base is something we have done before.
\[\begin{align}
& &&\ce{BNH2}\hspace{25px} +\hspace{25px} \ce{H2O} \hspace{25px}\leftrightarrow &&\ce{BNH3+} \hspace{25px} + &&\ce{OH-}\nonumber\\
&\ce{Initial} &&0.1 &&0 &&10^{-7}\nonumber\\
&\ce{Equilibrium} &&0.1 - \ce{x} &&\ce{x} &&\ce{x}\nonumber\\
&\ce{Approximation} &&0.1 &&\ce{x} &&\ce{x}\nonumber
\end{align}\nonumber\]
\[\mathrm{K_b = \dfrac{[BNH_3^+][OH^-]}{[BNH_2]} = \dfrac{(x)(x)}{0.1} = 3.98\times10^{-4}}\nonumber\]
\[\mathrm{x = [OH^-] = 6.31\times 10^{-3}}\nonumber\]
If we check the approximations:
\[\dfrac{10^{-7}}{6.31×10^{-3}}×100=0.0016\%\nonumber\]
\[\dfrac{6.31\times10^{-3}}{0.1} \times 100 = 6.31\%\nonumber\]
The first one is valid. The second one is not quite valid, but we’ll still use this value. Solving the quadratic would only lead to a small change in the initial value, and this is close enough for our purposes now.
\[\mathrm{pOH = 2.2}\nonumber\]
\[\mathrm{pH = 11.8}\nonumber\]
First thing we ought to ask is whether we think this is a reasonable number. Remembering that it is a base, a pH of 11.8 is basic, so that seems good.
Now we can examine the first 5 ml increment of hydrochloric acid that’s added. Remember that the HCl (shown as H3O+ in the reaction below since all of it is dissociated in water) will convert butylamine to butylammonium as shown below.
\[\ce{BNH2 + H3O+ \leftrightarrow BNH3+ + H2O}\nonumber\]
There is something else important to consider about this reaction. If we start with 30 ml of 0.1 M butylamine, that corresponds to 0.0030 moles. If we add 5 ml of 0.1 M hydrochloric acid, that corresponds to 0.0005 moles. The amounts of these initial reagents before and after the reaction are listed below
\[\begin{align}
& &&\ce{BNH2}\hspace{25px} + &&\ce{H3O+} \hspace{25px}\leftrightarrow &&\ce{BNH3+} \hspace{25px} + \hspace{25px}\ce{H2O}\nonumber\\
&\ce{Initial} &&\textrm{0.0030 mol} &&\textrm{0.0005 mol} &&0\nonumber\\
&\ce{After\:neutralization} &&\textrm{0.0025 mol} &&0 &&\textrm{0.0005 mol}\nonumber
\end{align}\nonumber\]
There is something very interesting to note about this solution. There are appreciable amounts of butylamine and butylammonium in the final solution. These two are a conjugate pair, so this solution is a buffer. We can solve for the pH of this solution by using the Henderson-Hasselbalch equation for butylamine.
But there is also something else that is interesting about this when you try to solve for the pH using the Henderson-Hasselbalch equation. If we examine the form of the Henderson-Hasselbalch equation, we note that the final term consists of the ratio of the concentrations of the two components of the buffer. Remember that we started with 30 ml of butylamine and added 5 ml of hydrochloric acid. This causes the final solution to have a volume of 35 ml. If we write out the terms in the equation as shown:
\[\mathrm{pH = pK_a + \log\left(\dfrac{[BNH_2]}{[BNH_3^+]} \right ) = 10.6 + \log\left(\dfrac{^{\Large{0.0025\: mol}}\Big/_{\Large{\cancel{35\:ml}}}}{^{\Large{0.0005\: mol}}\Big/_{\Large{\cancel{35\:ml}}}} \right ) = 11.3}\nonumber\]
What you note is that the two volume terms in the concentration ratio cancel each other out. In other words, the pH of a buffer solution can be calculated either by determining the ratio of the concentrations of the two components, or by determining the ratio of the moles of the two components.
There is another very important outcome of this. The pH of a buffer does not change if the solution is diluted. In other words, suppose we just added 5 ml of water to the above solution. The final volume would now be 40 ml, but the moles of each component would still be 0.0025 and 0.0005. The pH would remain the same because the volumes cancel. Now, does this hold under all circumstances? At some point if we diluted the solution too much, we may start to promote a significant redistribution of the two species in the buffer and this observation would break down. But generally, we find that the pH of a buffer solution stays fixed under dilution with water.
Before we go on to the next increment of hydrochloric acid, let’s consider one other aspect of this initial addition of 5 ml of acid. If we reconsider the initial solution, we found that x, which was the concentration of \(\ce{BNH3+}\), was 6.31\(\times\)10-3 M. If we calculate the moles of that we find out that it is:
\[\mathrm{[BNH_3^+] = \left(6.31\times 10^{-3}\: \dfrac{mol}{L}\right)(0.030\: L) = 0.0002\: moles}\nonumber\]
We could write these as the approximate amounts in the initial solution at equilibrium.
\[\begin{align}
&\ce{BNH2}\hspace{25px} + \hspace{25px}\ce{H2O} \hspace{25px}\leftrightarrow &&\ce{BNH3+} \hspace{25px} + &&\ce{OH-}\nonumber\\
&\textrm{0.0028 mol} &&\textrm{0.0002 mol} &&\textrm{0.0002 mol}\nonumber
\end{align}\nonumber\]
When we thought about adding the first 0.0005 moles of acid, we thought of it converting butylamine to butylammonium. Does that mean we should have removed 0.0005 moles of the 0.0028 moles that are listed under the reaction above? If so, that would alter the pH we got after the first addition. NO IT DOESN’T. We have to remember that 0.0002 moles of hydroxide are produced by this initial reaction. Hydroxide is a strong base and the first 0.0002 moles of hydrochloric acid will react with the hydroxide ion. The remaining 0.0003 moles of the acid will then start reacting with the butylamine.
The best way to proceed through the other increments of added hydrochloric acid is to construct a chart of the species in solution. This is shown in Table 1 with the first two pH values included.
Table 1. Moles of butylamine and butylammonium in the titration of butyl amine (0.1 M, 30 ml) with hydrochloric acid (0.1 M).
| Step # | Added HCl (ml) | BNH2 (moles) | \(\ce{BNH3+}\) (moles) | pH |
|---|---|---|---|---|
| 1 | 0 | 0.0030 | 0 | 11.8 |
| 2 | 5 | 0.0025 | 0.0005 | 11.3 |
| 3 | 10 | 0.0020 | 0.0010 | |
| 4 | 15 | 0.0015 | 0.0015 | |
| 5 | 20 | 0.0010 | 0.0020 | |
| 6 | 25 | 0.0005 | 0.0025 | |
| 7 | 30 | 0 | 0.0030 | |
| 8 | 35 | 0 | 0.0030 | |
| 9 | 40 | 0 | 0.0030 |
Examine the table and consider steps 3 through 6 (10 to 25 ml of acid added). In each of these cases, we have an appreciable amount of each of the two components of the conjugate pair and each of these solutions is a buffer. That means we can use the Henderson-Hasselbalch equation to solve for the pH. It is also sufficient to use the mole ratio of the two and not worry about the dilution of the molar concentrations that would occur.
\[\textrm{10 ml:} \hspace{60px} \mathrm{pH=10.6 + \log \left( \dfrac{0.0020\: mol}{0.0010\: mol}\right )= 10.9}\nonumber\]
\[\textrm{15 ml:} \hspace{60px} \mathrm{pH=10.6 + \log \left( \dfrac{0.0015\: mol}{0.0015\: mol}\right )= 10.6}\nonumber\]
Note an important point about this one. Here we have equal concentrations, or equal moles of the two components of the buffer, and the log of 1 is 0. At the point at which the concentrations of both members of the conjugate pair are equal, the pH of a buffer equals the pKa.
\[\textrm{20 ml:} \hspace{60px} \mathrm{pH=10.6 + \log \left( \dfrac{0.0010\: mol}{0.0020\: mol}\right )= 10.3}\nonumber\]
\[\textrm{25 ml:} \hspace{60px} \mathrm{pH=10.6 + \log \left( \dfrac{0.0005\: mol}{0.0025\: mol}\right )= 9.9}\nonumber\]
The situation at 30 mL of acid deserves some attention. First note, that this is called the equivalence point. The equivalence point is the point in a titration where the moles of titrant (hydrochloric acid) that have been added exactly equal the moles of analyte (butylamine) that were in the initial solution. It might be tempting to think that, since there are equal moles of acid and base, that the pH of a solution at the equivalence point of an acid-base titration must be 7. Let’s examine the solution that we have at the equivalence point of this titration.
To a first approximation, all of the butylamine has been used up and converted to butylammonium ion. This is the equivalent to saying what would be the pH of a solution prepared by adding some amount of butylammonium to water. If we think about the nature of butylammonium, we realize that it is a weak acid. So the solution at the equivalence point of this titration is a solution of a weak acid. If that’s the case, the pH at the equivalence point ought to be slightly acidic. Also note, that at this point we now have to account for the effects of dilution since we no longer have appreciable amounts of both members of the conjugate pair (we have 0.0030 moles of \(\ce{BNH3+}\) in a total volume of 60 ml or 0.060 L).
\[\mathrm{\dfrac{0.0030\: mol}{0.060\: L} = 0.050\: M}\nonumber\]
\[\begin{align}
& &&\ce{BNH3+}\hspace{25px} + \hspace{25px}\ce{H2O} \hspace{25px}\leftrightarrow &&\ce{BNH2} \hspace{25px} + &&\ce{H3O+}\nonumber\\
&\ce{Initial} &&0.05 &&0 &&10^{-7}\nonumber\\
&\ce{Equilibrium} &&0.05 - \ce{x} &&\ce{x} &&\ce{x}\nonumber\\
&\ce{Approximation} &&0.05 &&\ce{x} &&\ce{x}\nonumber
\end{align}\nonumber\]
\[\mathrm{K_a = \dfrac{[BNH_2][H_3O^+]}{[BNH_3^+]} = \dfrac{(x)(x)}{0.05} = 2.51\times10^{-11}}\nonumber\]
\[\mathrm{x = [H_3O^+] = 1.12\times 10^{-6}}\nonumber\]
\[\mathrm{pH = 5.9}\nonumber\]
Checking the approximation shows that it is valid.
\[\dfrac{1.12\times 10^{-6}}{0.05} \times 100 = 0.00224\%\nonumber\]
Note that the pH at this point, the equivalence point, is slightly acidic, just as we would expect for a solution of a weak acid. However, one other thing to note is that the true initial value of H3O+ at the equivalence point (10-7 M) is more than 5% of the final concentration of H3O+ (1.12\(\times\)10-6). So if we wanted to be rigorously correct, we would need to account for that in determining the true pH at the equivalence point.
If we now consider the solution where 35 ml of acid have been added, we note that the butylamine/butylammonium system is used up and no more changes can occur here. Instead, what we now have is an excess of strong acid. So this solution consists of a mixture of a weak acid (butylammonium) with some strong acid (hydrochloric). It should seem reasonable that the extra strong acid will be the critical part in determining the pH of the solution. Remember that every mole of HCl will be converted to H3O+.
5 ml of extra acid adds 0.0005 moles of H3O+.
\[\mathrm{\dfrac{0.0005\: mol}{0.065\: L} = 7.69\times 10^{-3}\: M\:\: [H_3O^+]}\nonumber\]
\[\mathrm{pH = 2.1}\nonumber\]
And for 40 ml:
10 ml of extra acid adds 0.0010 moles of H3O+.
\[\mathrm{\dfrac{0.0010\: mol}{0.070\: L} = 1.4 \times 10^{-2}\: M = [H_3O^+]}\nonumber\]
\[\mathrm{pH = 1.8}\nonumber\]
It’s worthwhile at this point to compile a complete table (Table 2) of this process and examine some of the general trends that occur.
Table 2. Calculated pH values for the titration of butyl amine (0.1 M, 30 ml) with hydrochloric acid (0.1 M).
| Step # | Added HCl (ml) | BNH2 (moles) | \(\ce{BNH3+}\) (moles) | pH |
|---|---|---|---|---|
| 1 | 0 ml | 0.0030 | 0 | 11.8 |
| 2 | 5 | 0.0025 | 0.0005 | 11.3 |
| 3 | 10 | 0.0020 | 0.0010 | 10.9 |
| 4 | 15 | 0.0015 | 0.0015 | 10.6 |
| 5 | 20 | 0.0010 | 0.0020 | 10.3 |
| 6 | 25 | 0.0005 | 0.0025 | 9.9 |
| 7 | 30 | 0 | 0.0030 | 5.9 |
| 8 | 35 | 0 | 0.0030 | 2.1 |
| 9 | 40 | 0 | 0.0030 | 1.8 |
First, note the large drop in pH between 25 and 30 ml of added acid. At this point we have exhausted the buffer and so it should not be surprising that a small amount of extra acid causes a large drop in pH. Also note, that the pH of 0.1 M hydrochloric acid is 1.0, so that the pH would slowly approach a limit of 1.0 if we continued to add more acid to the solution.
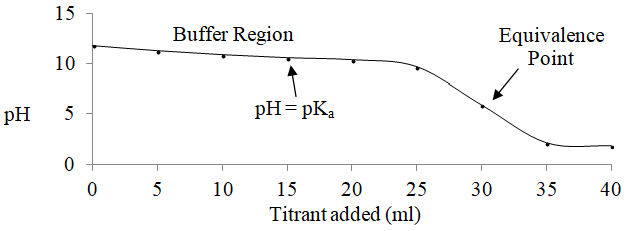
It is also worth examining a plot of the pH during the course of the titration as shown in Figure 1. The relatively flat portion of the plot between 5 ml and 25 ml of acid is known as the buffer region. Notice how the center of the buffer region corresponds to the pKa value. So the butylammonium/butylamine system would be a useful buffer at a pH of around 10.6.
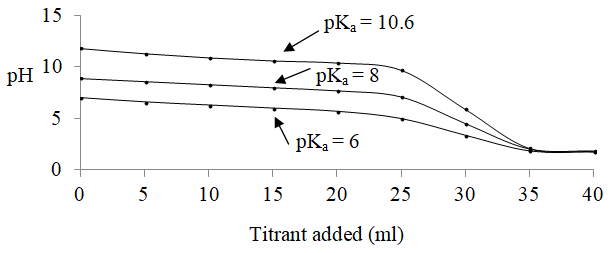
Suppose we had used an identical situation (30 ml of 0.1 M base, add 5 ml increments of HCl) but had a base whose conjugate acid had a pKa of 8. What would that plot look like? The plot is shown in Figure 2 and compared to what we observed with butylamine. Note how the initial pH would be a little less basic, how the buffer region is now centered around 8, how the equivalence point still occurs at 30 ml of acid, but how the pH at the equivalence point is a little more acidic because the weak acid is a little stronger than the butylammonium ion. If we then showed a plot for a species where the acid form had a pKa of 6, we start to note that it becomes more difficult to distinguish the equivalence point in the plot. A concentration of a species like butylamine can be analyzed using an acid-base titration. The concentration of a base whose conjugate acid has a pKa value of 6 could not be analyzed using an acid-base titration.
We can also talk about the qualities that define a “good” buffer. The term that is used here is buffer capacity (a measure of how much acid or base a buffer can neutralize without an appreciable change in pH), and we want a high buffer capacity.
Presumably there is a particular pH that you want to buffer your solution at. The first criteria is to select a buffer that has a pKa close to the pH that you want to buffer at. The “official standard” is that the pKa of the acid must be within +/– one unit of the pH you want to buffer at, but the closer the better. Note from the Henderson-Hasselbalch equation that one unit of change from pKa would correspond to either a 1/10 or 10/1 ratio of the two members of the conjugate pair. If you look at the plots above, note that ratios of 1/10 or 10/1 are out on the extreme end of the buffer region. At these extremes, there is a lot of buffer capacity in one direction, but almost none in the other. It would be risky to use such a solution as a buffer and much better to use a species with a pKa much closer to the pH you need to buffer at.
The second criterion is to have a high concentration of both components of the conjugate pair so that the buffer will neutralize more acid or base. A good buffer therefore is one in which both components of the conjugate pair are highly soluble in water. So buffers usually have high concentrations of species relative to the other species you are studying in solution. The actual concentration of components you use for a buffer depend on the nature of your investigation. In biochemistry, where the concentrations of proteins and nucleic acids are usually quite low, the concentrations of buffer components are relatively low. In chemical analysis procedures where the concentrations of reagents might be fairly high, the concentration of buffer needs to be high as well.
The last criteria in selecting a buffer is to ensure that the buffer components do not interfere in any way with the process being studied. For example, if you want to determine the amount of a substance in solution by measuring its absorption of light, it’s essential that the buffer not absorb at that wavelength. If your procedure involves the formation of a metal complex, it’s essential that the components of the buffer do not complex with the metal ion.
The criteria used in selecting a buffer can be summarized as follows:
- The buffer substance needs a pKa value as close as possible to the desired pH.
- The buffer components must have high solubility.
- The buffer components cannot interfere in any way with the other species in solution or the measurement you want to make.
Now, there is one other component to the question that we have not addressed yet. The question asks whether 99.9% of the butylamine has been titrated at the equivalence point (in other words, has 99.9% of the butylamine been converted to butylammonium). This is an important question in analysis procedures. If we used this titration to determine the concentration of butylamine in the solution, the assumption is that “all” of the butylamine has been converted to butylammonium so that we are getting an accurate measurement. Of course, we can never convert all of the butylamine, since the K values are finite and so there must always be a little bit of butylamine in the solution, but if we can convert at least 99.9%, that’s a high enough degree of accuracy for most purposes. The way we assess this is to compare the concentrations of the two species at the equivalence point. Going back to our pH calculation at 30 ml of acid, we have the following values:
\[\mathrm{[BNH_2] = 1.12 \times 10^{-6}\: M}\nonumber\]
\[\mathrm{[\ce{BNH3+}] = 0.05\: M}\nonumber\]
Admittedly, the \(\ce{BNH3+}\) is a little less than 0.05 M, but the approximation we made when solving the problem can still be used. If we evaluate the ratio of BNH2 to \(\ce{BNH3+}\), as shown below, we find that 0.002% is BNH2 and 99.998% is \(\ce{BNH3+}\) at the equivalence point. That says that this titration procedure would be an effective way to analyze the concentration of butylamine in the initial solution.
\[\dfrac{1.12\times10^{-6}}{0.05}\times 100 = 0.00224\%\nonumber\]
Contributors and Attributions
- Thomas Wenzel, Bates College (twenzel@bates.edu)
- Sourced from the Analytical Sciences Digital Library


