Section 3B. Time of Flight (TOF) Mass Analyzer
- Page ID
- 79444
This is set of questions guides students through the principle of a TOF mass analyzer. There is very little reading and all questions are for small group discussion.
(Source for figures and animations: Dr. Jon Karty of Indiana University Mass Spectrometry Facility)

Consider the diagram above, which shows 4 ions (the circles), between two electrical plates. The ions have different masses and higher mass is represented by a larger circle. Imagine the entire schematic is contained in a long tube under vacuum. After the ions enter, the left plate is brought to a positive high voltage (+HV) such as +15,000 V. The right plate is a grid, like a screen door, so that ions can pass through, and is held at electrical ground (0 V).
- In this scenario, the ions will accelerate once the +HV is applied. If the ions are positively charged, which direction will they move?
- If all of the ions have a charge of +1, which ion will reach the detector first? The larger circles represent ions with higher mass.
- What factors other than mass will influence the velocity of the ions?
- \[KE = zV \label{1}\]
where z is the charge on the ion and V is the magnitude of the high voltage (HV).
- Does this equation support your answer to number 3?
- If all of the ions have the same charge, what will be true about their kinetic energies?
- You may remember another equation for kinetic energy from physics:
where m is the mass of the object and v is its velocity.
- Consider the four ions at the start of this worksheet. Which ion will have the highest velocity?
- What is the order of ions reaching the detector?
- Is the TOF mass analyzer dispersive or scanning?
- Why do you think it is called a “time-of-flight” mass analyzer?
- Consider a +1 ion with m/z = 115 which enters the time-of-flight source region (between the two plates).
1 elementary charge = 1.6 × 10-19 C \(\mathrm{1\: V = 1\:\: \large{ {}^J/_C} }\)
- \(\mathrm{1\: J = 1\: \dfrac{kg \cdot m^2}{s^2}}\) 1 amu = 1.66 × 10-27 kg
- If the flight tube is 2 m long, how long will the ion take to reach the detector? Remember that v = d/t, where v is velocity, d is distance traveled, and t is time.
- The ability of a mass spectrometer to distinguish between two different m/z ions is called resolving power.
\(\textrm{Resolving Power} = \dfrac{m}{\Delta m}\)

Image adapted from UC Davis Fiehn Metabolomics Lab. fiehnlab.ucdavis.edu/projects...ass_Resolution
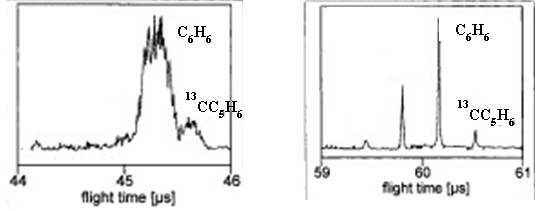
- Calculate the resolving power of the mass analyzer from the peak in the figure.
- Using the resolving power calculated in part (a), sketch the appearance of the two peaks with m/z ratios of 1500 and 1500.5. Would you say these peaks are resolved?
- Consider the two instrument schematics for a time of flight mass analyzer below. Which one do you think will be better at resolving small differences in the masses of the ions? Explain.
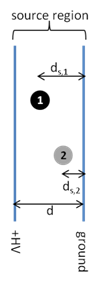
- Equation \(\ref{1}\) can also be written as:
where E is the electric field (V/d) and ds is the distance traveled in the source region. Use this equation to explain which ion (1 or 2) will leave the source with the highest velocity.
- How will the position of different ions in the source affect the resolving power of the mass analyzer? Draw a peak for a given m/z similar to the one in question 7 assuming that the position of the ion in the source did not affect kinetic energy. Draw a new peak taking into account how different positions of ions in the source affect the kinetic energy of the ions.
- Equation \(\ref{1}\) can also be written as:
- Consider the instrument diagram below, which adds a “reflectron” to the mass analyzer. The reflectron consists of a series of grids held at increasingly high positive potentials from ground (0 V) up to +HV2. Note: +HV2 > +HV1.
- On the diagram above, sketch the flight paths for Ion 1 and Ion 2 (these ions have the same m/z ratio and are the same ions in question 8). Note that the reflectron is angled toward the detector.
- Which ion penetrates farther into the reflectron?
- How does this arrangement correct for the ions’ different starting positions in the source?
- Examine the diagram of a reflectron TOF mass analyzer.
- What is the order of ions reaching the detector in the reflectron time of flight mass spectrometer? (all ions have a +1 charge)
- Why is the ionization method MALDI frequently coupled with a time of flight mass analyzer?
- Examine the two mass spectra below. Identify which spectrum is from a reflectron TOF instrument and which is from a linear TOF instrument?