Section 3B. Time of Flight (TOF) Mass Analyzer
- Page ID
- 80413
This set of questions guides students through the principle of a TOF mass analyzer. There is very little reading and all questions are for small group discussion.
(Source for figures and animations: Dr. Jon Karty of Indiana University Mass Spectrometry Facility)

Consider the diagram above, which shows 4 ions (the circles), between two electrical plates. The ions have different masses and higher mass is represented by a larger circle. Imagine the entire schematic is contained in a long tube under vacuum. After the ions enter, the left plate is brought to a positive high voltage (+HV) such as +15,000 V. The right plate is a grid, like a screen door, so that ions can pass through, and is held at electrical ground (0 V).
- A. They will move away from the plate because like charges repel.
- The powerpoint file, TOF Animations Slide 2 has a nice animation showing the answer to this question.
- Note: Most students will not know about the effect of distance through the electric field. This phenomena limits resolution and with be developed later on this worksheet.
- \[KE = zV \label{1}\]
where z is the charge on the ion and V is the magnitude of the high voltage (HV).
- Does this equation support your answer to number 3?
- If all of the ions have the same charge, what will be true about their kinetic energies?
- You may remember another equation for kinetic energy from physics:
where m is the mass of the object and v is its velocity.
- Consider the four ions at the start of this worksheet. Which ion will have the highest velocity?
- What is the order of ions reaching the detector?
- Is the TOF mass analyzer dispersive or scanning?
- Why do you think it is called a “time-of-flight” mass analyzer?
- Consider a +1 ion with m/z = 115 which enters the time-of-flight source region (between the two plates).
1 elementary charge = 1.6 × 10-19 C \(\mathrm{1\: V = 1\:\: \large{ {}^J/_C} }\)
A. KE = zV = (+1)(1.6 × 10-19 C)(2000 V) = 3.2 × 10-16 C . V = 3.2 × 10-16 J
- \(\mathrm{1\: J = 1\: \dfrac{kg \cdot m^2}{s^2}}\) 1 amu = 1.66 × 10-27 kg
\(KE = \left(\dfrac{1}{2} \right ) mv^2\)
\(3.2\times10^{-16}\dfrac{kg\cdot m^2}{s^2} = \left(\dfrac{1}{2} \right )(115\: amu)\left(\dfrac{1.66\times10^{-27}\:kg}{amu} \right )v^2\)
\(v = \mathrm{5.8\times 10^4\: m/s}\)
- A. 3.5 × 10-5 s or 35 μs
- The ability of a mass spectrometer to distinguish between two different m/z ions is called resolving power.
\(\textrm{Resolving Power} = \dfrac{m}{\Delta m}\)

Image adapted from UC Davis Fiehn Metabolomics Lab. fiehnlab.ucdavis.edu/projects...ass_Resolution
- A. \(\textrm{Resolving Power} = \dfrac{m}{\Delta m} = \dfrac{500.00}{0.10} = 5000 = 5.0 \times 10^3\)
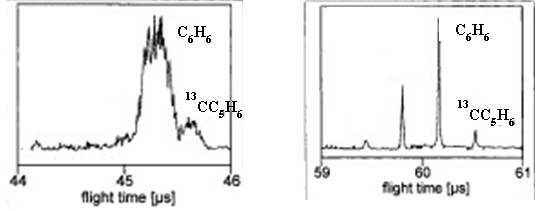
- A. The figure shows the appearance of the two peaks. They are resolved because they do not overlap at the baseline.
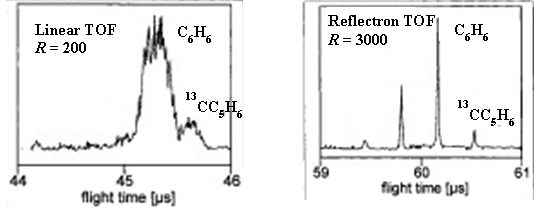
- Consider the two instrument schematics for a time of flight mass analyzer below. Which one do you think will be better at resolving small differences in the masses of the ions? Explain.
A. The longer flight tube will result in better resolution because the ions with different speeds will have more time to separate. Imagine two runners. One runner has a pace of 7:00 per mile, the other runner has a pace of 8:00 per mile. After 100 yards there will not be much separation between the two, but after a mile the separation will be much larger.
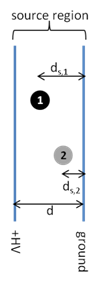
- A. Ion 1
\[KE=zEd_s \tag{3.1b}\]
where E is the electric field (V/d) and ds is the distance traveled in the source region. Use this equation to explain which ion (1 or 2) will leave the source with the highest velocity.
A. Ion 1 will be accelerated a larger distance through the electric field thus acquiring greater kinetic energy and velocity. The powerpoint file, TOF Animations, Slide 9 has a nice animation showing how the position of the ion in source affects the flight time.
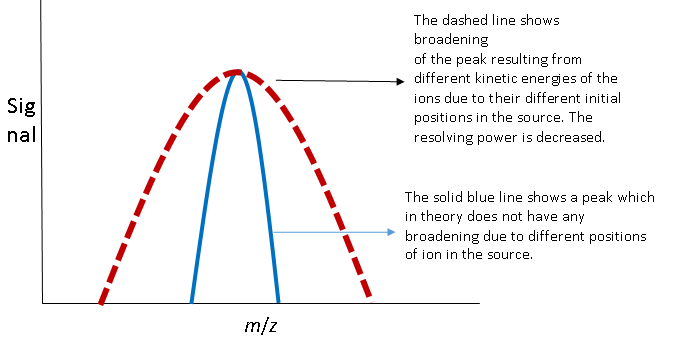
- How will the position of different ions in the source affect the resolving power of the mass analyzer? Draw a peak for a given m/z similar to the one in question 7 assuming that the position of the ion in the source did not affect kinetic energy. Draw a new peak taking into account how different positions of ions in the source affect the kinetic energy of the ions.
- A. Ion 1
- Consider the instrument diagram below, which adds a “reflectron” to the mass analyzer. The reflectron consists of a series of grids held at increasingly high positive potentials from ground (0 V) up to +HV2. Note: +HV2 > +HV1.
- A. Ion 1 and 2 turn around at the reflection and head toward the detector.
- A. Ion 1 will leave the source with greater kinetic energy and will be more difficult to stop and turn around. Therefore Ion 1 will penetrate further into the reflectron.
- A. Ion 1 is moving faster but travels a greater distance because it penetrates further into the reflectron. Ion 1 and Ion 2 should reach the detector at nearly the same time.
- Examine the diagram of a reflectron TOF mass analyzer.
- A. Lowest mass ion arrives first and highest mass ion arrives last. (red, blue, black, then yellow)
- A. To measure flight times a set of ions must enter the mass analyzer and be accelerated all at the same time. The pulsed nitrogen laser produces a “pulse” of ions for time of flight analysis. The nitrogen laser is often pulsed 100-200 times per second leading to improved signal to noise ratio due to signal averaging.