1.14: Auger Electron Spectroscopy
- Page ID
- 55832
Basic Principles
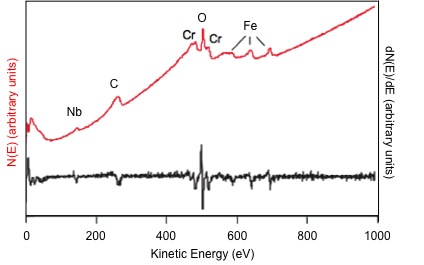
Auger electron spectroscopy (AES) is one of the most commonly employed surface analysis techniques. It uses the energy of emitted electrons to identify the elements present in a sample, similar to X-ray photoelectron spectroscopy (XPS). The main difference is that XPS uses an X-ray beam to eject an electron while AES uses an electron beam to eject an electron. In AES, the sample depth is dependent on the escape energy of the electrons. It is not a function of the excitation source as in XPS. In AES, the collection depth is limited to 1-5 nm due to the small escape depth of electrons, which permits analysis of the first 2 - 10 atomic layers. In addition, a typical analysis spot size is roughly 10 nm. A representative AES spectrum illustrating the number of emitted electrons, N, as a function of kinetic energy, E, in direct form (red) and in differentiated form (black) is shown in Figure \(\PageIndex{1}\).
Like XPS, AES measures the kinetic energy (Ek) of an electron to determine its binding energy (Eb). The binding energy is inversely proportional to the kinetic energy and can be found from \ref{1}, where hν is the energy of the incident photon and ΔΦ is the difference in work function between the sample and the detector material.
\[ E_{b}\ =\ h\nu \ -\ E_{k}\ +\ \Delta \Phi \label{1} \]
Since the Eb is dependent on the element and the electronic environment of the nucleus, AES can be used to distinguish elements and their oxidation states. For instance, the energy required to remove an electron from Fe3+ is more than in Fe0. Therefore, the Fe3+ peak will have a lower Ek than the Fe0 peak, effectively distinguishing the oxidation states.
Auger Process
An Auger electron comes from a cascade of events. First, an electron beam comes in with sufficient energy to eject a core electron creating a vacancy (see Figure \(\PageIndex{2}\)a). Typical energies of the primary electrons range from 3 - 30 keV. A secondary electron (imaging electron) of higher energy drops down to fill the vacancy (see Figure \(\PageIndex{2}\) b) and emits sufficient energy to eject a tertiary electron (Auger electron) from a higher shell (see Figure \(\PageIndex{2}\) c).
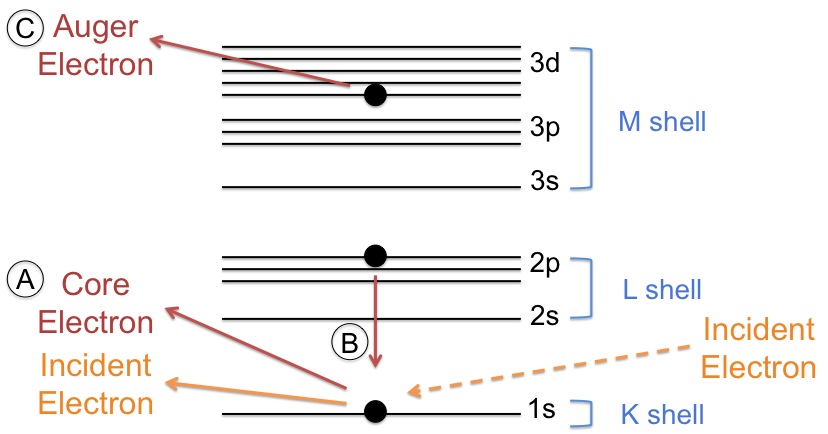
The shells from which the electrons move from lowest to highest energy are described as the K shell, L shell, and M shell. This nomenclature is related to quantum numbers. Explicitly, the K shell represents the 1s orbital, the L shell represents the 2s and 2p orbitals, and the M shell represents the 3s, 3p, and 3d orbitals. The cascade of events typically begins with the ionization of a K shell electron, followed by the movement of an L shell electron into the K shell vacancy. Then, either an L shell electron or M shell electron is ejected. It depends on the element, which peak is prevalent but often both peaks will be present. The peak seen in the spectrum is labeled according to the shells involved in the movement of the electrons. For example, an electron ejected from a gold atom could be labeled as Au KLL or Au KLM.
The intensity of the peak depends on the amount of material present, while the peak position is element dependent. Auger transitions characteristic of each elements can be found in the literature. Auger transitions of the first forty detectable elements are listed in Table \(\PageIndex{1}\).
| Atomic Number | Element | AES transition | Kinetic Energy of Transition (eV) |
|---|---|---|---|
| 3 | Li | KLL | 43 |
| 4 | Be | KLL | 104 |
| 5 | B | KLL | 179 |
| 6 | C | KLL | 272 |
| 7 | N | KLL | 379 |
| 8 | O | KLL | 508 |
| 9 | F | KLL | 647 |
| 11 | Na | KLL | 990 |
| 12 | Mg | KLL | 1186 |
| 13 | Al | LMM | 68 |
| 14 | Si | LMM | 92 |
| 15 | P | LMM | 120 |
| 16 | S | LMM | 152 |
| 17 | Cl | LMM | 181 |
| 19 | K | KLL | 252 |
| 20 | Ca | LMM | 291 |
| 21 | Sc | LMM | 340 |
| 22 | Ti | LMM | 418 |
| 23 | V | LMM | 473 |
| 24 | Cr | LMM | 529 |
| 25 | Mn | LMM | 589 |
| 26 | Fe | LMM | 703 |
| 27 | Co | LMM | 775 |
| 28 | Ni | LMM | 848 |
| 29 | Cu | LMM | 920 |
| 30 | Zn | LMM | 994 |
| 31 | Ga | LMM | 1070 |
| 32 | Ge | LMM | 1147 |
| 33 | As | LMM | 1228 |
| 34 | Se | LMM | 1315 |
| 35 | Br | LMM | 1376 |
| 39 | Y | MNN | 127 |
| 40 | Zr | MNN | 147 |
| 41 | Nb | MNN | 167 |
| 42 | Mo | MNN | 186 |
Instrumentation
Important elements of an Auger spectrometer include a vacuum system, an electron source, and a detector. AES must be performed at pressures less than 10-3 pascal (Pa) to keep residual gases from adsorbing to the sample surface. This can be achieved using an ultra-high-vacuum system with pressures from 10-8 to 10-9 Pa. Typical electron sources include tungsten filaments with an electron beam diameter of 3 - 5 μm, LaB6 electron sources with a beam diameter of less than 40 nm, and Schottky barrier filaments with a 20 nm beam diameter and high beam current density. Two common detectors are the cylindrical mirror analyzer and the concentric hemispherical analyzer discussed below. Notably, concentric hemispherical analyzers typically have better energy resolution.
Cylindrical Mirror Analyzer (CMA)
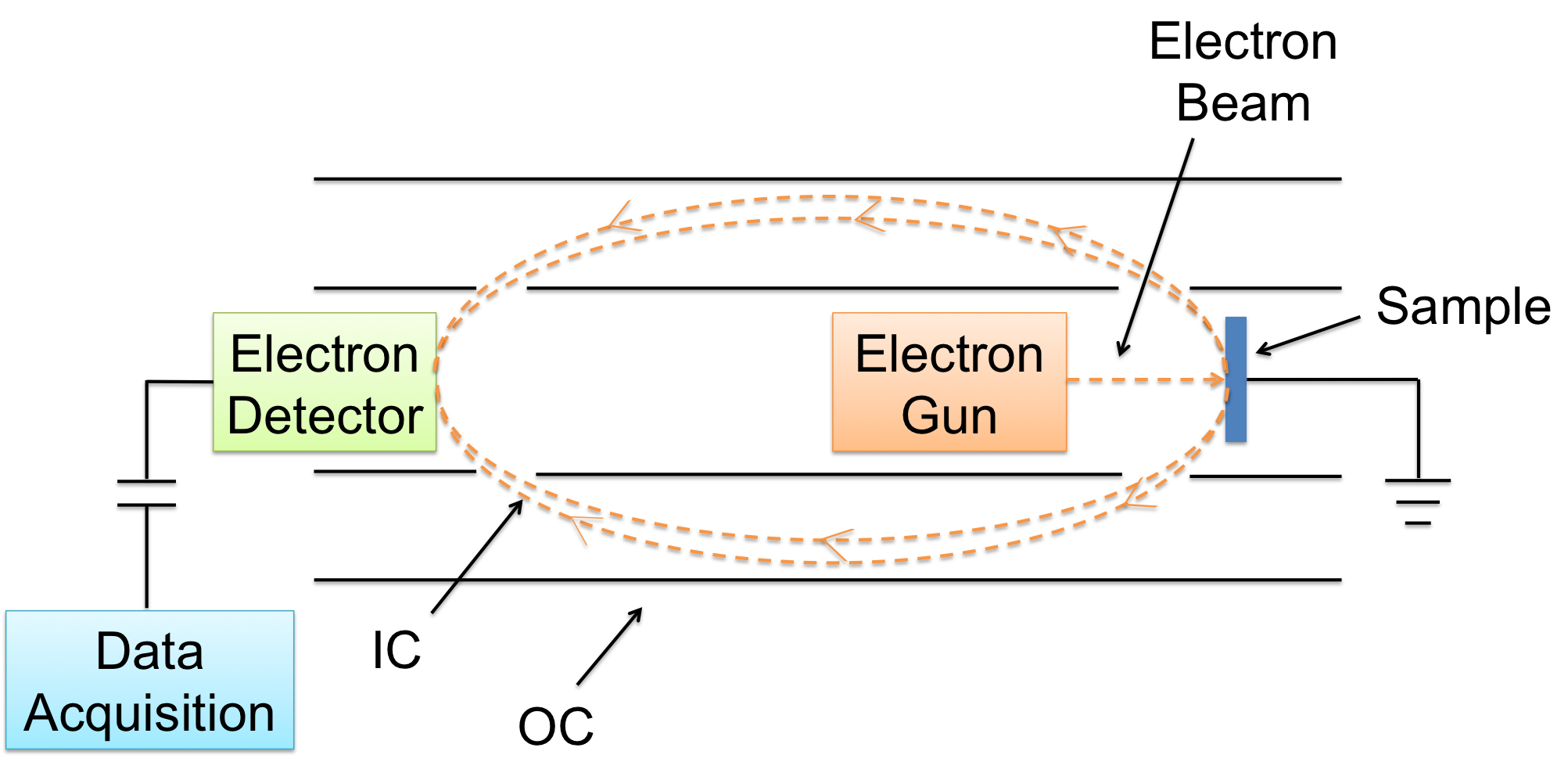
A CMA is composed of an electron gun, two cylinders, and an electron detector (Figure \(\PageIndex{2}\)). The operation of a CMA involves an electron gun being directed at the sample. An ejected electron then enters the space between the inner and outer cylinders (IC and OC). The inner cylinder is at ground potential, while the outer cylinder’s potential is proportional to the kinetic energy of the electron. Due to its negative potential, the outer cylinder deflects the electron towards the electron detector. Only electrons within the solid angle cone are detected. The resulting signal is proportional to the number of electrons detected as a function of kinetic energy.
Concentric Hemispherical Analyzer (CHA)
A CHA contains three parts (Figure \(\PageIndex{4}\)):
- A retarding and focusing input lens assembly
- An inner and outer hemisphere (IH and OH)
- An electron detector
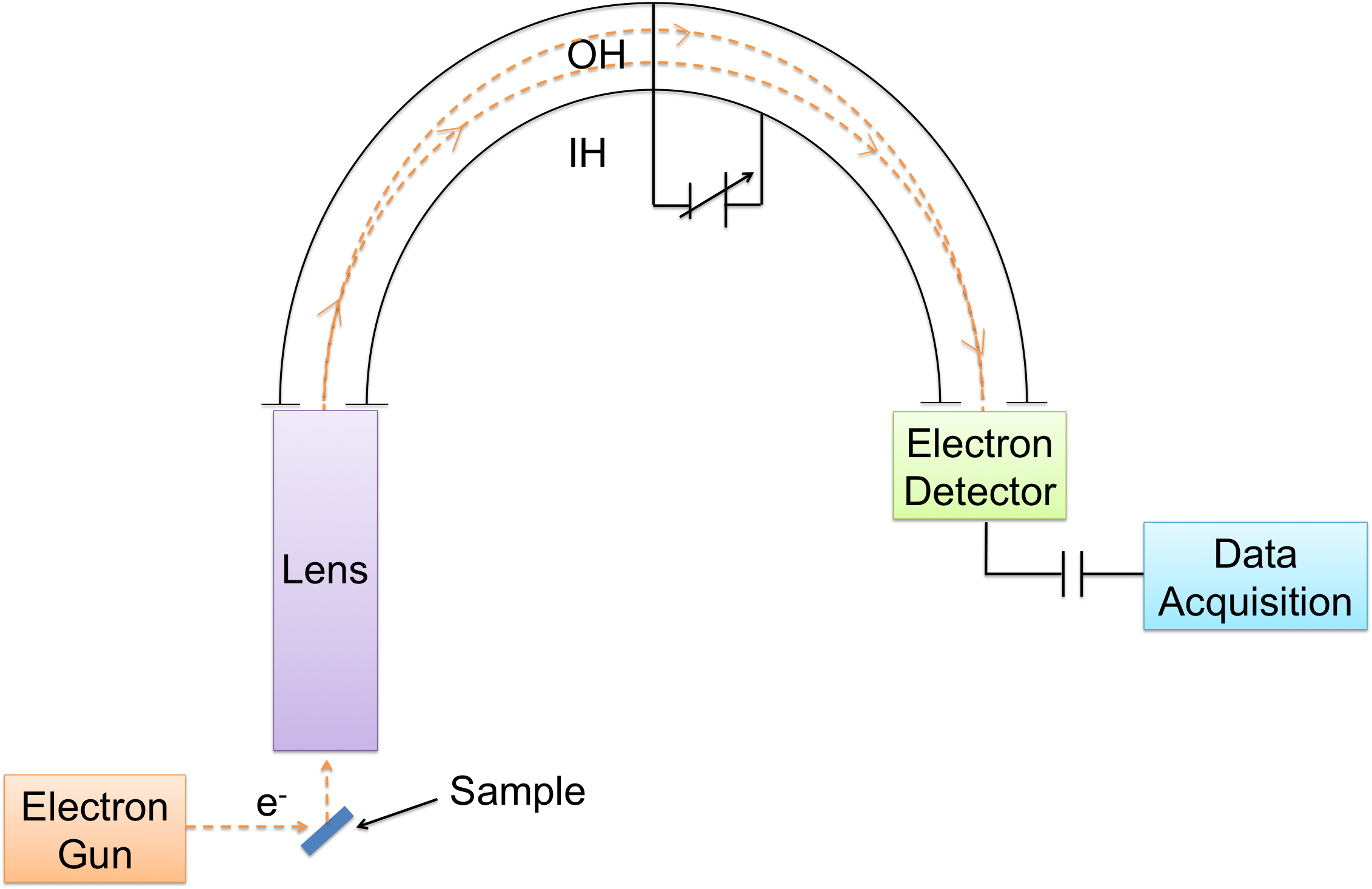
Electrons ejected from the surface enter the input lens, which focuses the electrons and retards their energy for better resolution. Electrons then enter the hemispheres through an entrance slit. A potential difference is applied on the hemispheres so that only electrons with a small range of energy differences reach the exit. Finally, an electron detector analyzes the electrons.
Applications
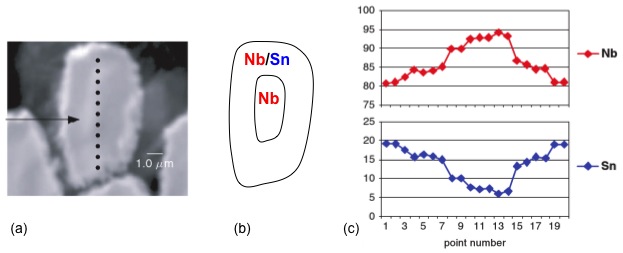
AES has widespread use owing to its ability to analyze small spot sizes with diameters from 5 μm down to 10 nm depending on the electron gun. For instance, AES is commonly employed to study film growth and surface-chemical composition, as well as grain boundaries in metals and ceramics. It is also used for quality control surface analyses in integrated circuit production lines due to short acquisition times. Moreover, AES is used for areas that require high spatial resolution, which XPS cannot achieve. AES can also be used in conjunction with transmission electron microscopy (TEM) and scanning electron microscopy (SEM) to obtain a comprehensive understanding of microscale materials, both chemically and structurally. As an example of combining techniques to investigate microscale materials, Figure \(\PageIndex{5}\) shows the characterization of a single wire from a Sn-Nb multi-wire alloy. Figure \(\PageIndex{5}\) a is a SEM image of the singular wire and Figure \(\PageIndex{5}\) b is a schematic depicting the distribution of Nb and Sn within the wire. Point analysis was performed along the length of the wire to determine the percent concentrations of Nb and Sn.
AES is widely used for depth profiling. Depth profiling allows the elemental distributions of layered samples 0.2 – 1 μm thick to be characterized beyond the escape depth limit of an electron. Varying the incident and collection angles, and the primary beam energy controls the analysis depth. In general, the depth resolution decreases with the square root of the sample thickness. Notably, in AES, it is possible to simultaneously sputter and collect Auger data for depth profiling. The sputtering time indicates the depth and the intensity indicates elemental concentrations. Since, the sputtering process does not affect the ejection of the Auger electron, helium or argon ions can be used to sputter the surface and create the trench, while collecting Auger data at the same time. The depth profile does not have the problem of diffusion of hydrocarbons into the trenches. Thus, AES is better for depth profiles of reactive metals (e.g., gold or any metal or semiconductor). Yet, care should be taken because sputtering can mix up different elements, changing the sample composition.
Limitations
While AES is a very valuable surface analysis technique, there are limitations. Because AES is a three-electron process, elements with less than three electrons cannot be analyzed. Therefore, hydrogen and helium cannot be detected. Nonetheless, detection is better for lighter elements with fewer transitions. The numerous transition peaks in heavier elements can cause peak overlap, as can the increased peak width of higher energy transitions. Detection limits of AES include 0.1 – 1% of a monolayer, 10-16 – 10-15 g of material, and 1012 – 1013 atoms/cm2.
Another limitation is sample destruction. Although focusing of the electron beam can improve resolution; the high-energy electrons can destroy the sample. To limit destruction, beam current densities of greater than 1 mA/cm2 should be used. Furthermore, charging of the electron beam on insulating samples can deteriorate the sample and result in high-energy peak shifts or the appearance of large peaks.


