2.3: BET Surface Area Analysis of Nanoparticles
- Page ID
- 55840
Introduction
In the past few years, nanotechnology research has expanded out of the chemistry department and into the fields of medicine, energy, aerospace and even computing and information technology. With bulk materials, the surface area to volume is insignificant in relation to the number of atoms in the bulk, however when the particles are only 1 to 100 nm across, different properties begin to arise. For example, commercial grade zinc oxide has a surface area range of 2.5 to 12 m2/g while nanoparticle zinc oxide can have surface areas as high as 54 m2/g . The nanoparticles have superior UV blocking properties when compared to the bulk material, making them useful in applications such as sunscreen. Many useful properties of nanoparticles rise from their small size, making it very important to be able to determine their surface area.
Overview of BET Theory
The BET theory was developed by Stephen Brunauer (Figure \(\PageIndex{1}\) ), Paul Emmett (Figure \(\PageIndex{2}\) ), and Edward Teller (Figure \(\PageIndex{3}\) ) in 1938. The first letter of each publisher’s surname was taken to name this theory. The BET theory was an extension of the Langmuir theory, developed by Irving Langmuir (Figure \(\PageIndex{4}\) ) in 1916.




The Langmuir theory relates the monolayer adsorption of gas molecules (Figure \(\PageIndex{5}\) ), also called adsorbates, onto a solid surface to the gas pressure of a medium above the solid surface at a fixed temperature to \ref{1} , where θ is the fractional cover of the surface, P is the gas pressure and α is a constant.
\[ \Theta \ =\ \frac{\alpha \cdot P}{1\ +\ (\alpha \cdot P)} \label{1} \]
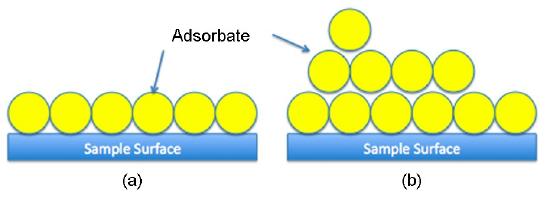
The Langmuir theory is based on the following assumptions:
- All surface sites have the same adsorption energy for the adsorbate, which is usually argon, krypton or nitrogen gas. The surface site is defined as the area on the sample where one molecule can adsorb onto.
- Adsorption of the solvent at one site occurs independently of adsorption at neighboring sites.
- Activity of adsorbate is directly proportional to its concentration.
- Adsorbates form a monolayer.
- Each active site can be occupied only by one particle.
The Langmuir theory has a few flaws that are addressed by the BET theory. The BET theory extends the Langmuir theory to multilayer adsorption (Figure \(\PageIndex{1}\) ) with three additional assumptions:
- Gas molecules will physically adsorb on a solid in layers infinitely.
- The different adsorption layers do not interact.
- The theory can be applied to each layer.
How does BET Work?
Adsorption is defined as the adhesion of atoms or molecules of gas to a surface. It should be noted that adsorption is not confused with absorption, in which a fluid permeates a liquid or solid. The amount of gas adsorbed depends on the exposed surface are but also on the temperature, gas pressure and strength of interaction between the gas and solid. In BET surface area analysis, nitrogen is usually used because of its availability in high purity and its strong interaction with most solids. Because the interaction between gaseous and solid phases is usually weak, the surface is cooled using liquid N2 to obtain detectable amounts of adsorption. Known amounts of nitrogen gas are then released stepwise into the sample cell. Relative pressures less than atmospheric pressure is achieved by creating conditions of partial vacuum. After the saturation pressure, no more adsorption occurs regardless of any further increase in pressure. Highly precise and accurate pressure transducers monitor the pressure changes due to the adsorption process. After the adsorption layers are formed, the sample is removed from the nitrogen atmosphere and heated to cause the adsorbed nitrogen to be released from the material and quantified. The data collected is displayed in the form of a BET isotherm, which plots the amount of gas adsorbed as a function of the relative pressure. There are five types of adsorption isotherms possible.
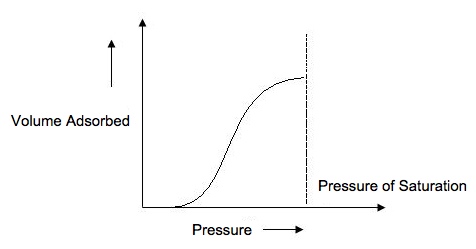
Type I Isotherm
Type I is a pseudo-Langmuir isotherm because it depicts monolayer adsorption (Figure \(\PageIndex{6}\) ). A type I isotherm is obtained when P/Po < 1 and c > 1 in the BET equation, where P/Po is the partial pressure value and c is the BET constant, which is related to the adsorption energy of the first monolayer and varies from solid to solid. The characterization of microporous materials, those with pore diameters less than 2 nm, gives this type of isotherm.
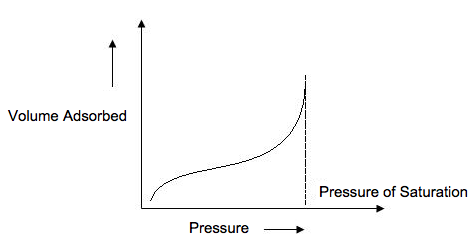
Type II Isotherm
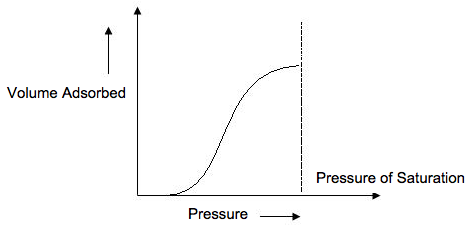
A type II isotherm (Figure \(\PageIndex{7}\) ) is very different than the Langmuir model. The flatter region in the middle represents the formation of a monolayer. A type II isotherm is obtained when c > 1 in the BET equation. This is the most common isotherm obtained when using the BET technique. At very low pressures, the micropores fill with nitrogen gas. At the knee, monolayer formation is beginning and multilayer formation occurs at medium pressure. At the higher pressures, capillary condensation occurs.
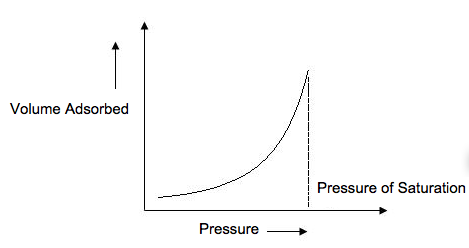
Type III Isotherm
A type III isotherm (Figure \(\PageIndex{8}\) ) is obtained when the c < 1 and shows the formation of a multilayer. Because there is no asymptote in the curve, no monolayer is formed and BET is not applicable.
Type IV Isotherm
Type IV isotherms (Figure \(\PageIndex{9}\) ) occur when capillary condensation occurs. Gases condense in the tiny capillary pores of the solid at pressures below the saturation pressure of the gas. At the lower pressure regions, it shows the formation of a monolayer followed by a formation of multilayers. BET surface area characterization of mesoporous materials, which are materials with pore diameters between 2 - 50 nm, gives this type of isotherm.
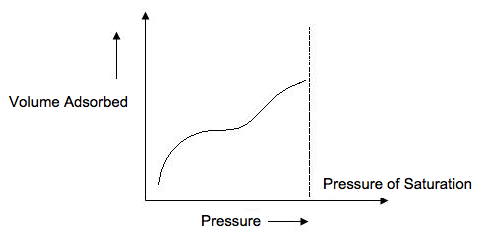
Type V Isotherm
Type V isotherms (Figure \(\PageIndex{10}\) ) are very similar to type IV isotherms and are not applicable to BET.
Calculations
The BET Equation, \ref{2} , uses the information from the isotherm to determine the surface area of the sample, where X is the weight of nitrogen adsorbed at a given relative pressure (P/Po), Xm is monolayer capacity, which is the volume of gas adsorbed at standard temperature and pressure (STP), and C is constant. STP is defined as 273 K and 1 atm.
\[ \frac{1}{X[(P_{0}/P)-1]} = \frac{1}{X_{m}C} + \frac{C-1}{X_{m}C} (\frac{P}{P_{0}}) \label{2} \]
Multi-point BET
Ideally five data points, with a minimum of three data points, in the P/P0 range 0.025 to 0.30 should be used to successfully determine the surface area using the BET equation. At relative pressures higher than 0.5, there is the onset of capillary condensation, and at relative pressures that are too low, only monolayer formation is occurring. When the BET equation is plotted, the graph should be of linear with a positive slope. If such a graph is not obtained, then the BET method was insufficient in obtaining the surface area.
- The slope and y-intercept can be obtained using least squares regression.
- The monolayer capacity Xm can be calculated with \ref{3} .
- Once Xm is determined, the total surface area St can be calculated with the following equation, where Lav is Avogadro’s number, Am is the cross sectional area of the adsorbate and equals 0.162 nm2 for an absorbed nitrogen molecule, and Mv is the molar volume and equals 22414 mL, \ref{4} .
\[ X_{m}\ = \frac{1}{s\ +\ i} = \frac{C-1}{C_{s}} \label{3} \]
\[S\ = \frac{X_{m} L_{av} A_{m}}{M_{v}} \label{4} \]
Single point BET can also be used by setting the intercept to 0 and ignoring the value of C. The data point at the relative pressure of 0.3 will match up the best with a multipoint BET. Single point BET can be used over the more accurate multipoint BET to determine the appropriate relative pressure range for multi-point BET.
Sample Preparation and Experimental Setup
Prior to any measurement the sample must be degassed to remove water and other contaminants before the surface area can be accurately measured. Samples are degassed in a vacuum at high temperatures. The highest temperature possible that will not damage the sample’s structure is usually chosen in order to shorten the degassing time. IUPAC recommends that samples be degassed for at least 16 hours to ensure that unwanted vapors and gases are removed from the surface of the sample. Generally, samples that can withstand higher temperatures without structural changes have smaller degassing times. A minimum of 0.5 g of sample is required for the BET to successfully determine the surface area.
Samples are placed in glass cells to be degassed and analyzed by the BET machine. Glass rods are placed within the cell to minimize the dead space in the cell. Sample cells typically come in sizes of 6, 9 and 12 mm and come in different shapes. 6 mm cells are usually used for fine powders, 9 mm cells for larger particles and small pellets and 12 mm are used for large pieces that cannot be further reduced. The cells are placed into heating mantles and connected to the outgas port of the machine.
After the sample is degassed, the cell is moved to the analysis port (Figure \(\PageIndex{11}\) ). Dewars of liquid nitrogen are used to cool the sample and maintain it at a constant temperature. A low temperature must be maintained so that the interaction between the gas molecules and the surface of the sample will be strong enough for measurable amounts of adsorption to occur. The adsorbate, nitrogen gas in this case, is injected into the sample cell with a calibrated piston. The dead volume in the sample cell must be calibrated before and after each measurement. To do that, helium gas is used for a blank run, because helium does not adsorb onto the sample.
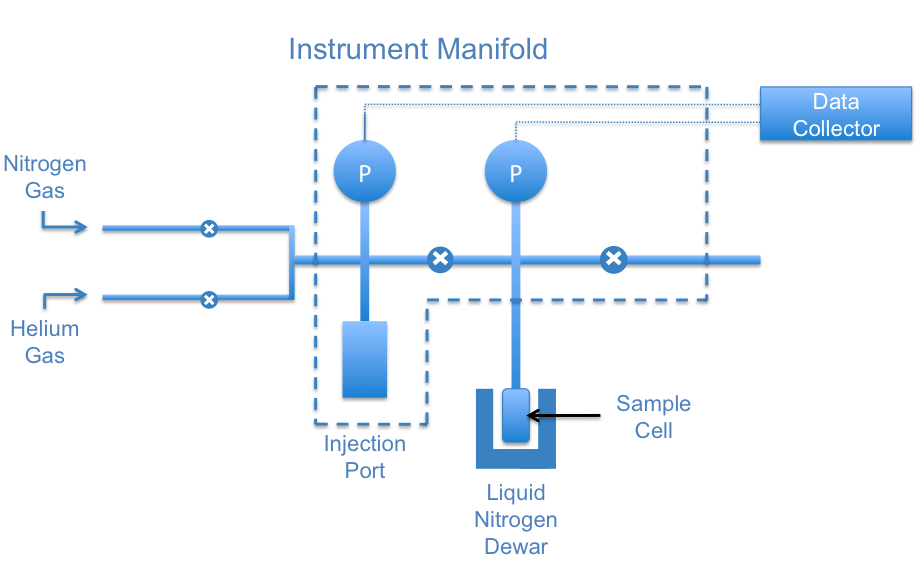
Shortcomings of BET
The BET technique has some disadvantages when compared to NMR, which can also be used to measure the surface area of nanoparticles. BET measurements can only be used to determine the surface area of dry powders. This technique requires a lot of time for the adsorption of gas molecules to occur. A lot of manual preparation is required.
The Surface Area Determination of Metal-Organic Frameworks
The BET technique was used to determine the surface areas of metal-organic frameworks (MOFs), which are crystalline compounds of metal ions coordinated to organic molecules. Possible applications of MOFs, which are porous, include gas purification and catalysis. An isoreticular MOF (IRMOF) with the chemical formula Zn4O(pyrene-1,2-dicarboxylate)3 (Figure \(\PageIndex{12}\) ) was used as an example to see if BET could accurately determine the surface area of microporous materials. The predicted surface area was calculated directly from the geometry of the crystals and agreed with the data obtained from the BET isotherms. Data was collected at a constant temperature of 77 K and a type II isotherm (Figure \(\PageIndex{13}\) ) was obtained.
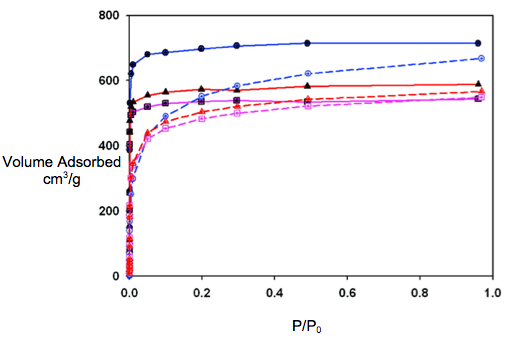
The isotherm data obtained from partial pressure range of 0.05 to 0.3 is plugged into the BET equation, \ref{2} , to obtain the BET plot (Figure \(\PageIndex{14}\) ).
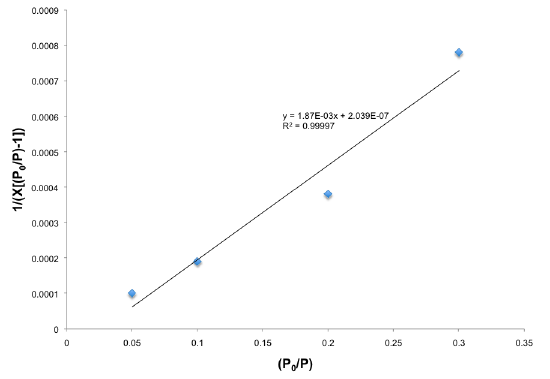
Using \ref{5} , the monolayer capactiy is determined to be 391.2 cm3/g.
\[ X_{m}\ = \frac{1}{(2.66E\ -\ 3)\ +\ (-5.212E\ -\ 0.05)} \label{5} \]
Now that Xm is known, then \ref{6} can be used to determine that the surface area is 1702.3 m2/g.
\[S\ =\frac{391.2cm^{2} \ast 0.162nm^{2} \ast 6.02\ast 10^{23}}{22.414:L} \label{6} \]


