9.5: J-Couplings and Spectral Intensities

V. J-Couplings and Spectral Intensities

The spectral lines of ethanol in Figure 3 exhibit fine structure -- i.e. the -CH₃ line consists of three lines and the -CH₂- has four components² . This coupling occurs because each magnetic nucleus also contributes to the local field of adjacent nuclei -- an effect referred to as spin-spin coupling. The strength of this coupling is described by a field independent coupling constant, J, measured in Hertz (Hz).

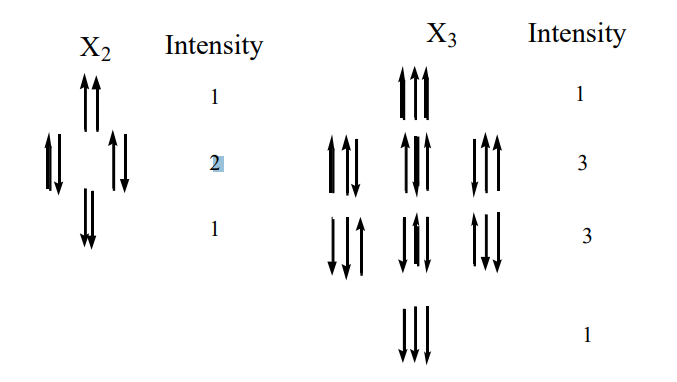
Figure 5: (a) Orientations of the spins in the X₂ group (-CH₂-) of an AX₂ spin system which give rise to a 1:2:1 triplet in the A resonance. The two nuclei may have the 2² = 4 spin arrangements shown. (b) The 2³ = 8 arrangements of the three spins in an AX₃ group, which lead to the 1:3:3:1 quartet in the A resonance.

The spectral pattern in Figure 3 can be understood by examining the simple diagrams shown in Figure 5. If two spins that correspond to the two ¹H's on a -CH₂- are present, they can be aligned in four different ways. Each spin is either parallel or opposed to the field. Therefore, two spins can be aligned both up, both down, and one up and one down (in two different ways: spin one up/spin two down, and spin one down/spin two up). Thus, the local field at the -CH₃ due to the adjacent -CH₂- should have three components with an intensity ratio of 1:2:1, corresponding to both up, one up and one down (2 ways), and both down. Correspondingly, there are eight ways to align the three spins on the methyl group, as illustrated in the figure, resulting in a quartet for the -CH₂- with intensities of 1:3:3:1. By extending these arguments to larger numbers of spins, it is possible to show that N equivalent spins split the resonance of a coupled group into N+1 lines, with intensities corresponding to the coefficients of a binomial expansion or Pascal's Triangle. A Pascal's triangle is shown on the following page, where N is the total number of equivalent spins.

The size of J-couplings depends on the structure and the nuclei involved. ¹ H-¹ H couplings are ~10 Hz, while ¹ H-¹³C and ³¹P-¹ H couplings can be ~100 Hz. and ~600 Hz, respectively.

Another noteworthy feature of Figure 3 is the integrated spectral intensity of each set of lines. The integrals, which are performed electronically in an experiment, are shown as the steplike curves in the figure and are in the ratio 1:2:3, corresponding to the number of each type of ¹ H present. Thus, intensities in ¹ H spectra can be employed to determine the relative numbers of each type of ¹ H present in a molecule.

In summary, chemical shifts and spectral intensities provide information on the types and number of nuclei, respectively, associated with each functional group present in a molecule. Further J-couplings permit a determination of which groups are chemically bonded. Together these parameters permit the structures of most organic molecules to be determined by simply recording and interpreting their NMR spectra.

 

 

Footnotes

² J.T. Arnold, Phys. Rev. 102, 136 (1955).