9.4: Chemical Shifts

Last updated
Save as PDF

Page ID: 212006

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

IV. Chemical Shifts

Every nucleus in a molecule is surrounded by an electron cloud, which possesses an electronic angular momentum induced by the laboratory field, B₀. This angular momentum results in a local magnetic field, B_loc , at the nucleus, which is opposed to the applied field because it arises from negatively charged electrons. Putting a molecule into a magnetic field causes the electrons to circulate inducing a current that has a magnetic field associated with it. Thus, the induced magnetic field from the micro current of circulating electrons shields the nucleus from the applied field according to the following formula where σ is the shielding constant.

\[ \rm B_{loc} = (1 - \sigma) B_0\]

So, the net field felt at each nucleus (B_loc) is less than the applied field. The feature that makes NMR so interesting and extremely important to chemists is that σ varies markedly from chemical group to chemical group. Thus, σ for a -C1 H3 is different from σ for a -C¹H₂-, and that in turn is different from σ for an -O¹H. These features of NMR spectra, illustrated for the ¹H's in ethanol in Figure 3, are referred to as chemical shifts. They are important since they facilitate the identification of each type of 1 H (or 13C) present in a molecule.

All of the shifts in Figure 3 are referenced to the shift of the standard tetramethylsilane (TMS) and are calculated from the formula:

\[ \delta = \dfrac{\nu_0 - \nu_{ref}}{\nu_{ref}} \times 10^6\]

where, ν₀ and ν_ref is the frequency of the unknown and reference (TMS), respectively. As mentioned above, the amount of shielding, and therefore the frequency separation between two lines, will increase with increasing field. However, the chemical shifts calculated from Equation (6) are field independent. Thus, shifts measured at 100 MHz can be compared directly with those obtained at 500 MHz. Note that positive δ values correspond to higher frequencies or lower magnetic fields.

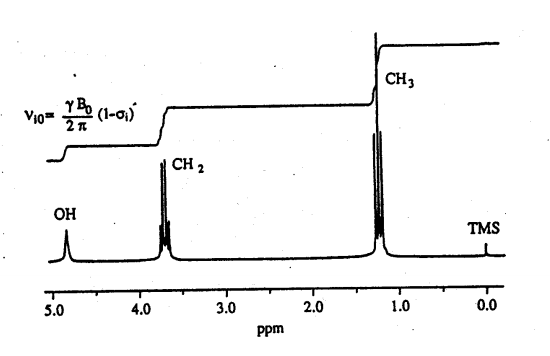
Figure 3.png

Figure 3 – The proton NMR spectrum of ethanol. TMS (the rightmost signal) stands for tetramethylsilane (Si(CH₃)₄). TMS is the widely-used reference signal. The step-like curve is the integrated signal, proportional to the number of spins in each signal. J.T. Arnold and co-workers first recorded this spectrum in 1951 [Journal of Chemical Physics 19, p. 507].

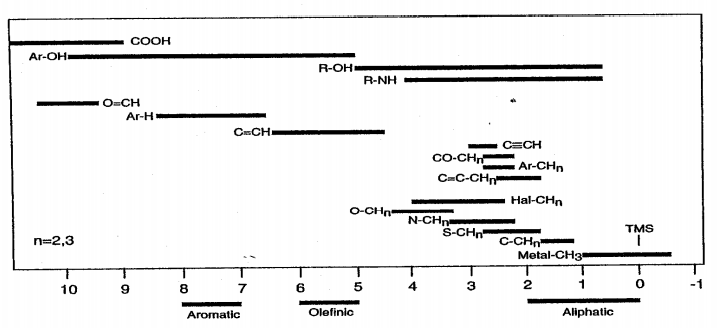
Figure 4 illustrates the dependence of proton chemical shifts on the various functional groups in more detail. Note that Figure 4b also shows chemical shifts for ¹³C, another important NMR nucleus.

(a)

Figure 4a.png

(b)

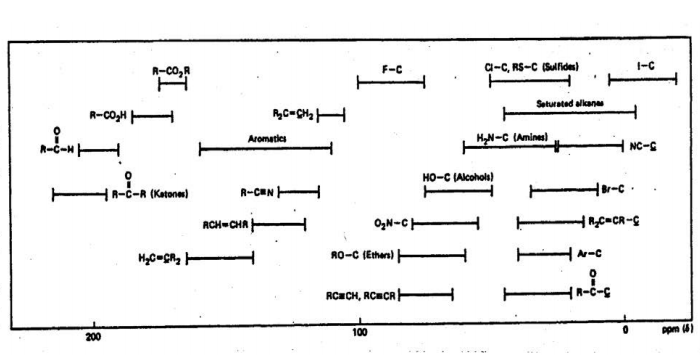
Figure 4b.png

Figure 4: Bar graph illustrating the range of chemical shifts expected for various types of (a) ¹H resonances and (b) ¹³C resonances, referenced to TMS.