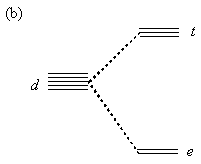Cisplatin 6. Transition Metal Chemistry
- Page ID
- 2903
The transition metals, also called the d-block elements, are found in groups 3-12 of the periodic table. These elements make the transition between the representative metals in groups 1 and 2 and the metalloids, representative metals, and nonmetals in groups 13-18. Moreover, it is in this block of elements in the periodic table that the d-orbitals are being filled with electrons. For example, elements in the first group of the d-block (group 3 of the periodic table: scandium, yttrium, lanthanum, and actinium) each have one d-electron. Likewise, elements in the eighth group of the d-block (group 10 of the periodic table: nickel, palladium, and platinum) each have eight d-electrons when in the +2 oxidation state
The transition metals have several features in common: unlike representative metals, most transition metals have variable valence, meaning that they have more than one possible oxidation—or valence—state. For example, platinum exists most commonly in the +2 and +4 oxidation states, but it can also be found in the +5 and +6 oxidation states.

Another common feature of the transition metals is their size. To understand why the d-metals are roughly the same size, we need to examine two competing effects: nuclear charge and electron-electron repulsions. As one moves across the periodic table, the size (that is, the atomic radius) of elements generally decreases due to increasing nuclear charge. The increasing nuclear charge is usually more significant than the electron-electron repulsions resulting from the addition of electrons as one moves across a period. In keeping with this trend, transition metals also generally decrease in size as one moves from left to right across the d-block. Here, the exceptionally weak shielding offered by the d-electrons causes these electrons to experience a greater nuclear charge and be pulled more strongly toward the nucleus. The last few elements in each row of the d-block are slightly larger than those preceding them; here, electron-electron repulsions outweigh increasing nuclear charge as the d-orbitals are filled. The trend of decreasing size is most pronounced in row 6 of the periodic table (the third row of the d-block, in which the 5d-orbitals are being filled). The third row of the d-block is interrupted by the lanthanide elements, in which the 4f-orbital is being filled. Like d-electrons, electrons in f-orbitals are also ineffective at shielding nuclear charge; the increased nuclear charge in the third row transition metals causes them to be smaller than expected and virtually identical in size to the second row transition metals.
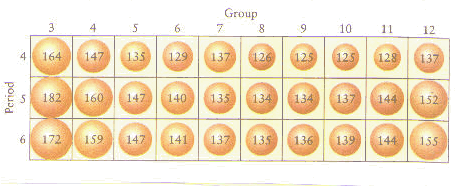
In addition to making the third row transition metals smaller, the lanthanide contraction also makes them less reactive because the valence electrons are relatively close to the nucleus and not available for chemical reactions. In short, several generalizations may be made about the transition metals, or d-metals: most transition metals have a number of possible oxidation states. Also, the d-metals are all roughly the same size. This is particularly noticeable when comparing the second and third row d-metals. Due to the lanthanide contraction, the third row d-metals are approximately the same size as the second row d-metals; the lanthanide contraction also causes the third row d-metals to be relatively inert. The inertness of the third row transition metals has many benefits. For example, these metals—particularly gold and platinum—are often used in jewelry. Furthermore, these metals—specifically, platinum—should be able to conduct an electric current but not react with their surroundings. For this reason, Barnett Rosenberg and his coworkers chose platinum as an electrode material in their original experiments to study the effect of electric fields on E. coli. However, as we have seen in the module on the role of platinum electrodes, even though their choice was based on sound chemical principles, they obtained unexpected results, which led to the serendipitous discovery of cisplatin.
Transition Metal Complexes1 Transition metals are excellent Lewis acids and accept electron density from many molecules or ions that act as Lewis bases; when a Lewis base donates its electron pair to a Lewis acid, it is said to coordinate to the Lewis acid and form a coordinate covalent bond. When Lewis bases coordinate to metals acting as Lewis acids and form an integral structural unit, a coordination compound is formed. In this type of compound, or complex, the Lewis bases are called ligands. One of the first known coordination compounds was Peyrone’s Chloride (also known as cis-diamminedichloroplatinum(II), or cis-DDP), first reported in 1845. This compound was not fully understood until 1893, when Alfred Werner deduced its structure and described cis-DDP and its trans isomer in a landmark paper.
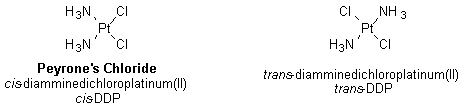
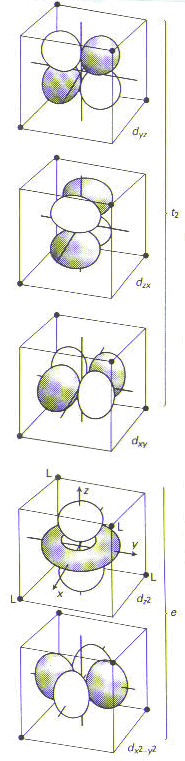
The two isomers of diamminedichloroplatinum(II) have the same connectivity of atoms, meaning that platinum is the central atom and is bonded to four ligands—two chlorine atoms and two amino groups—in a square planar arrangement. However, the ligands are arranged differently in the cis and trans isomers: In cis-DDP, the ammonia molecules are on the same side of the DDP molecule, but in trans-DDP, the ammonia molecules are on opposite sides of the DDP molecule. These types of isomers are called geometrical isomers. Crystal Field Theory1-3 It is possible to imagine several ways that four ligands can be arranged around a central metal atom. Werner deduced that the ligands in cis- and trans-DDP were placed at the corners of a square, with the platinum atom at the center of the square; this is called square planar geometry. Another way that four ligands could have been arranged around the central platinum atom would have been at the corners of a tetrahedron; this is referred to as tetrahedral geometry (and is the geometry adopted by carbon atoms having four substituents in organic compounds). In tetrahedral geometry, however, no isomers are possible, whereas with square planar geometry, two isomers are possible and can be identified, as shown above. To understand why different four-coordinate complexes (that is, those having four ligands around a central metal atom) adopt different geometries, we use the concepts described by crystal field theory (CFT), first proposed in 1929 by Hans Bethe. CFT uses an electrostatic model to explain all metal ion-ligand interactions. (A subsequent theory—called ligand field theory—builds on the principles of CFT and allows for some covalency, as well. CFT, however, will suffice to explain the geometries of various four-coordinate complexes.) Because CFT bases all interactions on electrostatics, each ligand is represented by a negative point charge. The way these point charges interact with the d-orbitals of a metal atom explains the geometries adopted by various transition metal complexes. In the absence of ligands (meaning in the absence of a crystal field), all d-orbitals in a particular metal have the same energy and are said to be degenerate. When ligands coordinate to the metal, however, the ligands (treated as point charges) cause the d-orbitals to be either stabilized or destabilized. A stabilizing effect from a ligand lowers the energy of the interacting d-orbital, whereas a destabilizing effect raises the energy of the d-orbital. Before we address the question of different four-coordinate geometries, it is useful to examine a very common geometry in transition metal complexes: the six-coordinate, octahedral geometry. In an octahedral complex, six ligands are placed symmetrically along the axes of a Cartesian coordinate system (the x-, y-, and z-axes in three-dimensional space), with the metal at the origin. Knowing the shapes of the five d-orbitals is essential in understanding octahedral geometry. As shown in Figure 3(a), there are two d-orbitals that point directly along Cartesian axes: the dz2 orbital, which points along the z-axis, and the dx2-y2 orbital, which has lobes on both the x- and y-axes. The interaction of six ligands with the dz2 and the dx2-y2 orbitals raises the energy of these two d-orbitals through repulsive interactions. Moreover, the energy of these two orbitals is increased by the same amount, so the dz2 and the dx2-y2 orbitals are degenerate. In the nomenclature of crystal field theory, these orbitals are called the e orbitals. The other three d-orbitals, the dxy, dzx, and dyz orbitals, which all have lobes in between the Cartesian axes, are repelled less by the ligands and are in effect stabilized to a lower energy. The dxy, dzx, and dyz orbitals are also degenerate; collectively, they are called the t orbitals. (See Figure 3(b).)
a)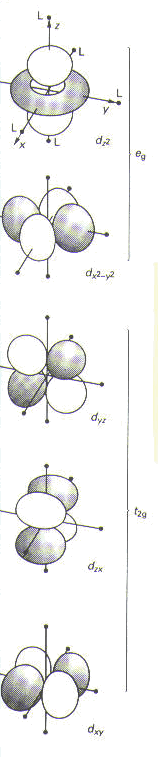 |
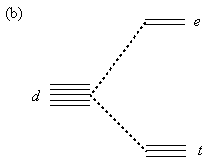 |
Figure 3. (a) The orientation of the five d-orbitals with respect to the ligands of an octahedral complex: the degenerate e pair, and the degenerate t triplet. Reprinted with permission.3 (b) Splitting of the five d-orbitals by an octahedral field.
We use similar logic to explain the crystal field splitting of the d-orbitals in a four-coordinate, tetrahedral complex. One way to represent a tetrahedral species is to show four ligands (treated as point charges in crystal field theory) on alternating corners of a cube. In a tetrahedral complex, the ligands do not point directly at any of the five d-orbitals, but they come close to the dxy, dzx, and dyz orbitals, which are directed toward the edges of the cube, as shown in Figure 4(a); these orbitals are raised in energy and are degenerate. The dz2 and the dx2-y2 orbitals point toward the sides of the cube and are therefore directed away from the attached ligands; these two orbitals are lowered in energy and are degenerate. The relative energies (and crystal field splitting) of the five d-orbitals in a tetrahedral complex are shown in Figure 4(b).
(a)
Figure 4. (a) The effect of a tetrahedral crystal field on a set of d-orbitals is to split them into two sets; the e pair (which point less directly at the ligands) lie lower in energy than the t triplet. Reprinted with permission.3 (b) Splitting of the five d-orbitals by a tetrahedral field.
Crystal field theory also explains the four-coordinate, square planar geometry. In this case, we imagine an octahedral complex in which the ligands on the z-axis (that is, those interacting most directly with the dz2 orbital) are removed. The dz2 orbital is therefore lowered in energy. Furthermore, the other d-orbitals having z-character—specifically, the dzx and dyz orbitals—also decrease in energy. However, since the ligands are all now in the xy plane, both d-orbitals having x- and y-character—namely, the dx2-y2 and the dxy orbitals—are raised in energy. The crystal field splitting pattern of a square planar complex is shown in Figure 5.
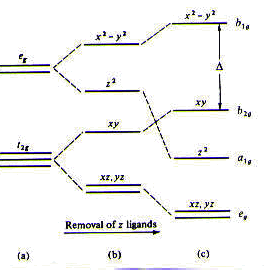
What determines whether a four-coordinate transition metal complex is tetrahedral or square planar? The answer lies in the number of d-electrons in the central transition metal. If the metal has eight d-electrons, as is the case for Pt2+, it is energetically advantageous for the complex to adopt a square planar geometry. In this case, the eight d-electrons will achieve some stabilization in energy by occupying the dzx, dyz, dz2, and dxy orbitals. < face="Arial">Formation of Cisplatin under the Experimental Conditions Now that we have some background in transition metal chemistry, particularly transition metal complexes, we can understand how cisplatin, or cis-diamminedichloroplatinum(II), was generated under the original reaction conditions in which elongation of E. coli bacterial cells was observed. As we saw in the electrochemistry module, a divalent platinum ion (Pt2+) could be generated when an electric current was supplied to the supposedly inert platinum electrodes in the continuous culture chamber. Moreover, as we saw in the control experiments module, solutions containing either ammonium ion or chloride ion or both tested positive for the presence of an oxidizing agent using the potassium iodide–starch test. One of the oxidizing agents present—namely, cis-diamminedichloroplatinum(II)—was responsible for bacterial elongation. How does cis-PtII(NH3)2Cl2 form from Pt2+, NH4+, and Cl- ions? Remember that in an aqueous solution, ammonium ion (NH4+) is in equilibrium with its conjugate base, ammonia (NH3):
\[NH_4^+ \rightleftharpoons NH_3 + H^ \nonumber \]
Assuming that sufficient concentrations of Pt2+, NH3, and Cl- ions exist in solution, the square planar cisplatin molecule will be formed:
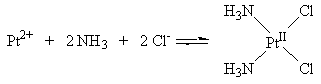
< face="Arial">Speaking the Language of Transition Metal Chemistry—Vocabulary
- Coordinate: Use of a lone pair to form a coordinate covalent bond Coordinate covalent bond: A bond formed between a Lewis base and a Lewis acid by sharing an electron pair originally belonging to the Lewis base
- Coordination compound: A compound in which a metal ion or atom is bonded to one or more molecules or anions so as to define an integral structural unit
- Ligand: A group attached to a central metal ion in a complex
- Isomer: One of two or more compounds that contain the same number of the same atoms in different arrangements Stereoisomers: Isomers that have the same connectivity of atoms but differ in the arrangement of their parts in space (identical atom-to-atom bonding but different arrangements of the atoms in space)
- Geometrical isomers: Stereoisomers that differ in the spatial arrangement of the atoms
- Crystal field: The electrostatic influence of the ligands (modeled as negative point charges) on the central ion of a complex
- Degenerate: Having the same energy, as in orbitals
- Octahedral complex: A complex in which six ligands are arranged at the corners of a regular octahedron with the metal atom at the center
- Tetrahedral complex: A complex in which four ligands lie at the corners of a regular tetrahedron with the metal atom at the center
- Square planar complex: A complex in which four ligands lie at the corners of a square with the metal atom at the center.
References
- Atkins, P. W., Jones, L. L. Chemistry: Molecules, Matter, and Change, 3rd ed. W. H. Freeman and Company: New York, 1997, Chapter 21.
- Huheey, J. E., Keiter, E. A., Keiter, R. L. Inorganic Chemistry: Principles of Structure and Reactivity, 4th ed. HarperCollins College Publishers: New York, 1993, Chapter 11.
- Shriver, D. F., Atkins, P., Langford, C. H. Inorganic Chemistry, 2nd ed. W. H. Freeman and Company: New York, 1994, Chapter 6.