5.3: Math in Chemistry

Skills to Develop

• Use the factor-label method to solve problems.
• Perform metric conversions using the factor-label method for conversions.

During your studies of chemistry (and physics also), you will note that mathematical equations are used in a number of different applications. Many of these equations have a number of different variables with which you will need to work. You should also note that these equations will often require you to use measurements with their units. Algebra skills become very important here!

Conversion Factors

A conversion factor is a factor used to convert one unit of measurement into another. A simple conversion factor can be used to convert meters into centimeters, or a more complex one can be used to convert miles per hour into meters per second. Since most calculations require measurements to be in certain units, you will find many uses for conversion factors. What always must be remembered is that a conversion factor has to represent a fact; this fact can either be simple or much more complex. For instance, you already know that 12 eggs equal 1 dozen. A more complex fact is that the speed of light is \(1.86 \times 10^5\) miles/\(\text{sec}\). Either one of these can be used as a conversion factor depending on what type of calculation you might be working with.

Factor-Label Method of Problem Solving

Frequently, it is necessary to convert units measuring the same quantity from one form to another. For example, it may be necessary to convert a length measurement in meters to millimeters. This process is quite simple if you follow a standard procedure called unit analysis or dimensional analysis. The Factor-Label Method is a technique that involves the study of the units of physical quantities. It affords a convenient means of checking mathematical equations. This method involves considering both the units you presently have (given measurement) and the units you wish to end up with, and designing conversion factors that will cancel units you don't want and produce units you do want. The conversion factors are created from the equivalency relationships between the units or ratios of how units are related to each other.

In terms of making unit conversions, suppose you want to convert 0.0856 meters into millimeters. In this case, you need only one conversion factor and that conversion factor must cancel the meters unit and create the millimeters unit. The conversion factor will be created from the relationship \(1000\) millimeters (\(\text{mm}\)) \(=\) \(1\) meter (\(\text{m}\)).

\[0.0856 \: \cancel{\text{m}} \cdot \frac{1000 \: \text{mm}}{1 \: \cancel{\text{m}}} = 85.6 \: \text{mm}\]

Remember that when you multiply fractions and you have the same number on top of one fraction and the bottom of another fraction, the numbers will cancel out leaving one. The same is true for units. When the above expression is multiplied as indicated, the meters units will cancel out and only millimeters will remain. The unit analysis process involves creating conversion factors from equivalencies between various units.

The given tables contain many useful conversion factors.

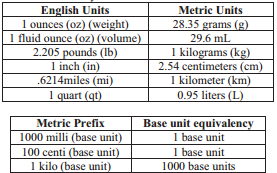
Of course, there are other ratios which are not listed in these tables. They may include:

• Ratios embedded in the test of the problem (using words such as per or in each, or using symbols such as / or %).
• Conversions in the metric system, as covered earlier in this chapter.
• Common knowledge ratios (such as 60 seconds \(=\) 1 minute).

The general steps you must take in order to solve these problems include:

1. Identify the "given" information in the problem. Look for a number with units to start this problem with.
2. What is the problem asking you to "find"? In other words, what unit will your answer have?
3. Use ratios and conversion factors to cancel out the units that aren't part of your answer, and leave you with units that are part of your answer.
4. When your units cancel out correctly, you are ready to do the math. You are multiplying fractions, so you multiply the top numbers and divide by the bottom numbers in the fractions.

Look for each of these steps in the following examples.

Example 5.3.1

Convert 1.53 grams to centigrams.

Solution

The equivalency relationship is \(100 \: \text{cg} = 1 \: \text{g}\) (given in the second table), so the conversion factor is constructed from this equivalency to cancel grams and produce centigrams.

\[1.53 \: \cancel{\text{g}} \cdot \frac{100 \: \text{cg}}{1 \: \cancel{\text{g}}} = 153 \: \text{cg}\]

Example 5.3.2

Convert 1000 inches to feet.

Solution

The equivalency between inches and feet is \(12 \: \text{inch} = 1 \: \text{ft}\). The conversion factor is designed to cancel out inches and produce feet.

\[1000 \: \cancel{\text{inch}} \cdot \frac{1 \: \text{ft}}{12 \: \cancel{\text{inch}}} = 83 \: \text{ft}\]

Each conversion factor is designed specifically for the problem. In this case, we know we need to cancel out inches so we need the inches component in the conversion facto to be in the denominator.

Sometimes, it is necessary to insert a series of conversion factors. Suppose we need to convert miles to kilometers and the only equivalencies we know are \(1 \: \text{mile} = 5280 \: \text{ft}\), \(12 \: \text{inch} = 1 \: \text{ft}\), \(2.54 \: \text{cm} = 1 \: \text{inch}\), \(100 \: \text{cm} = 1 \: \text{m}\), and \(1000 \: \text{m} = 1 \: \text{km}\). We will set up a series of conversion factors so that each conversion factor produces the next unit in the sequence.

Example 5.3.3

Convert 12 miles to kilometers.

Solution

Although we have a ratio for miles to kilometers given in the table, we will solve this problem using other units to see what a longer process looks like. The answer would be the same.

\[12 \: \cancel{\text{mile}} \cdot \frac{5280 \: \cancel{\text{ft}}}{1 \: \cancel{\text{mile}}} \cdot \frac{12 \: \cancel{\text{inch}}}{1 \: \cancel{\text{ft}}} \cdot \frac{2.54 \: \cancel{\text{cm}}}{1 \: \cancel{\text{inch}}} \cdot \frac{1 \: \cancel{\text{m}}}{100 \: \cancel{\text{cm}}} \cdot \frac{1 \: \text{km}}{1000 \: \cancel{\text{m}}} = 19 \: \text{km}\]

In each step, the previous unit is canceled and the next unit in the sequence is produced, each successive unit canceling out until only the unit needed in the answer is left.

Conversion factors for area and volume can also be produced by this method.

Example 5.3.4

Convert \(1500 \: \text{cm}^2\) to \(\text{m}^2\).

Solution:

\[1500 \: \cancel{\text{cm}}^2 \cdot \left( \frac{1 \: \text{m}}{100 \: \cancel{\text{cm}}} \right)^2 = 0.15 \: \text{m}^2\]

or

\[1500 \: \cancel{\text{cm}}^2 \cdot \left( \frac{1 \: \text{m}^2}{10,000 \: \cancel{\text{cm}}^2} \right) = 0.15 \: \text{m}^2\]

Summary

• Conversion factors are used to convert one unit of measurement into another.
• The factor-label method involves considering both the units you presently have and the units you wish to end up with, and designing conversion factors that will cancel units you don't want and produce units you do want.

Vocabulary

• Conversion factor: A ratio used to convert one unit of measurement into another.

Further Reading/Supplemental Links

• Tutorial: Vision Learning: Unit Conversions & Dimensional Analysis http://visionlearning.com/library/mo...?mid=144&1=&c3=

Contributors