9.9: Reactions in Solution
- Last updated
- Save as PDF
- Page ID
- 3537
Learning Objectives
Make sure you thoroughly understand the following essential ideas:
- Describe some of the major differences between the kinetics of reactions in the gas phase, compared with those in liquid solutions.
- What role do solvent cages play in solution kinetics?
- Explain the distinction between diffusion-control and activation-control of reaction rates in solutions.
- How can the polarity of a solvent affect the energetics of a reaction mechanism?
The kinetics fundamentals we covered in the earlier sections of this lesson group relate to processes that take place in the gas phase. But chemists and biochemists are generally much more concerned with solutions. This lesson will take you through some of the extensions of basic kinetics that you need in order to understand the major changes that occur when reactions take place in liquid solutions.
What's different about kinetics in liquid solutions?
Most of the added complications of kinetics and rate processes in liquid solutions arise from the much higher density of the liquid phase. In a typical gas at atmospheric pressure, the molecules occupy only about 0.2 per cent of the volume; the other 99.8 percent is empty space. In a liquid, molecules may take up more than half the volume, and the "empty" spaces are irregular and ever-changing as the solvent molecules undergo thermal motions of their own.

In a typical liquid solution, the solvent molecules massively outnumber the reactant solute molecules, which tend to find themselves momentarily (~10–11 sec) confined to a "hole" within the liquid. This trapping becomes especially important when the solvent is strongly hydrogen-bonded as is the case with water or alcohol.
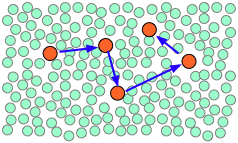
When thermal motions occasionally release a solute molecule from this trap, it will jump to a new location. The jumps are very fast (10–12 - 10–13 sec) and short (usually a few solvent-molecule diameters), and follow an entirely random pattern, very much as in Brownian motion. Consider a simple bimolecular process A + B → products. The reactant molecules will generally be jumping from hole to hole in the solvent matrix, only occasionally finding themselves in the same solvent cage where thermal motions are likely to bring them into contact.
 |
 |
 |
 |
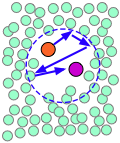
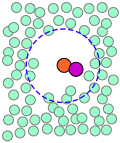
| A pair of reactants end up in the same solvent cage, where they bounce around randomly and exchange kinetic energy with the solvent molecules. | Eventually the two reactants form an encounter pair. If they fail to react the first time, they have many more opportunities during the lifetime of the cage. | The products form and begin to move away from each other. | Finally, after about 10–11 sec, the solvent cage breaks up and the products diffuse away. |
The process can be represented as
\[A + B \rightarrow \{AB\} → \text{products}\]
in which the \(\{AB\}\) term represents the caged reactants including the encounter pair and the activated complex.
Contrast this scenario with a similar reaction taking place in the gas phase; the molecules involved in the reaction will often be the only ones present, so a significant proportion of the collisions will be \(A\)-\(B\) encounters. However, if the collision should fail to be energetically or geometrically viable, the reactant molecules fly apart and are unlikely to meet again anytime soon. In a liquid, however, the solute molecules are effectively in a constant state of collision — if not with other reactants, then with solvent molecules which can exchange kinetic energy with the reactants. So once an A-B encounter pair forms, the two reactants get multiple whacks at each other, greatly increasing the probability that they will obtain the kinetic energy needed to kick them over the activation hump before the encounter pair disintegrates.
Limiting Cases: Diffusion-Controlled and Activation-Controlled Reactions
The encounter pair model introduces some new rate parameters:
\[\ce{A + B <=>[k1][k_{-1}] {AB} -> products}\]
The first step is an equilibrium between the reactants outside and inside the solvent cage. The rate constants \(k_1\) and \(k_2\) reflect those relating to diffusion of molecules through the solvent; their values are strongly dependent on the viscosity (and thus the temperature) of the solvent. (Note that \(k_1\) is a second-order rate constant, while \(k_2\) is first-order.)
Diffusion is the transport of a substance through a concentration gradient; that is, from a region of higher concentration to one of lower concentration. Think of the way the color of tea spreads out when a tea bag is immersed in hot water. Diffusion occurs because random thermal motions are statistically more likely to move molecules out of a region of higher concentration than in the reverse direction, simply because in the latter case fewer molecules are available to make the reverse trip. Eventually the concentrations become uniform and equilibrium is attained.
As molecules diffuse through a liquid, they must nudge neighboring molecules out of the way. The work required to do this amounts to an activation energy, so diffusion can be thought of as a kinetic process with its own rate constant kd and activation energy. These parameters depend on the sizes of the solute and solvent molecules and on how strongly the latter interact with each other. This suggests two important limiting cases for reactions in solution.
For water at room temperature, k1 is typically 109-1010 dm–3 mol–1 s–1 and k2 is around 10–9-10–10 dm–3 mol–1 s–1. Given these values, k3 > 1012 s–1 implies diffusion control, while values < 109 s–1 are indicative of activation control.
- Diffusion Controlled (\(k_3 \gg k_2\)): If the activation energy of the A+B reaction is very small or if escape of molecules from the {AB} cage is difficult, the kinetics will be dominated by k1, and thus by the activation energy of diffusion. Such a process is said to be diffusion controlled. Reactions in aqueous solution in which Ea > 20 kJ/mol are likely to fall into this category.
- Activation Controlled (\(k_3 \ll k_2\)): Alternatively, if the activation energy of the A+B reaction dominates the kinetics, and the reaction is activation-controlled.
Several general kinds of reactions are consistently very "fast" and thus are commonly found to be diffusion-controlled in most solvents:
Units Matter
Gas-phase rate constants are normally expressed in units of mol s–1, but rate constants of reactions in solution are conventionally given in mol/L units, or dm3 mol–1 s–1. Conversion between them depends on a number of assumptions and is non-trivial.
- Recombination of atoms and radicals
For example the formation of I2 from I atoms in hexane at 298 K has k3 = 1.3×1012 dm3 mol–1 s–1.
- Acid-base reactions which involve the transport of H+ and OH– ions tend to be very fast.
The most famous of these is one of the fastest reactions known:\[H^+ + OH^– → H_2O \nonumber \] for which k3 = 1.4×1011 dm3 mol–1 s–1 at 298 K.
Polar solvents such as water and alcohols interact with ions and polar molecules through attractive dipole-dipole and ion-dipole interactions, leading to lower-energy solvated forms which stabilize these species. In this way, a polar solvent can alter both the thermodynamics and kinetics (rate) of a reaction.
Solvent Thermodynamic Effect
If the products of the reaction are markedly more or less polar than the reactants, solvent polarity can change the overal thermodynamics (equilibrium constant) of the reaction. Nowhere is this more apparent than when an ionic solid such as salt dissolves in water. The Na+ and Cl– ions are bound together in the solid through strong coulombic forces; pulling the solid apart in a vacuum or in a nonpolar solvent is a highly endothermic process. In contrast, dissolution of NaCl in water is slightly exothermic and proceeds spontaneously.
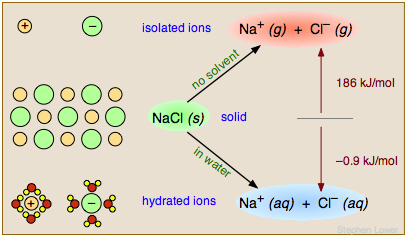
The water facilitates this process in two important ways. First, its high dielectric constant of 80 reduces the force between the separated ions to 1/80 of its normal value. Secondly, the water molecules form a solvation shell around the ions (lower left), rendering them energetically (thermodynamically) more stable than they were in the NaCl solid.
Solvent Kinetic Effect
In the same way, a reaction whose mechanism involves the formation of an intermediate or activated complex having a polar or ionic character will have its activation energy, and thus its rate, subject to change as the solvent polarity is altered. As an example we will consider an important class of reactions that you will hear much about if you take a course in organic chemistry. When an aqueous solution of a strong base such as KOH is added to a solution of tertiary-butyl chloride in ethanol, the chlorine is replaced by a hydroxyl group, leaving t-butyl alcohol as a product:
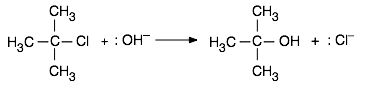
This reaction is one of a large and important class known as SN1 nucleophilic substitution processes that are discussed in most organic chemistry courses. In these reactions, a species that possesses a pair of non-bonding electrons (also called a nucleophile or Lewis base) uses them to form a new bond with an electrophile — a compound in which a carbon atom has a partial positive charge owing to its bonds to electron-withdrawing groups. In the example here, other nucleophiles such as NH3 or even H2O would serve as well.
In order to reflect the generality of this process and to focus on the major changes that take place, we will represent this reaction as
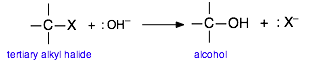
Extensive studies of this class of reactions in the 1930's revealed that it proceeds in two activation energy-controlled steps, followed by a simple dissociation into the products:

In step  , which is rate-determining, the chlorine leaves the alkyl chloride which becomes an intermediate known as a carbocation ("cat-ion"). These ions, in which the central carbon atom lacks a complete octet, are highly reactive, and in step
, which is rate-determining, the chlorine leaves the alkyl chloride which becomes an intermediate known as a carbocation ("cat-ion"). These ions, in which the central carbon atom lacks a complete octet, are highly reactive, and in step  the carbocation is attacked by the hydroxide ion which supplies the missing electron. The immediate product is another cation in which the positive charge is on the oxygen atom. This oxonium ion is unstable and rapidly dissociates (
the carbocation is attacked by the hydroxide ion which supplies the missing electron. The immediate product is another cation in which the positive charge is on the oxygen atom. This oxonium ion is unstable and rapidly dissociates ( )into the alcohol and a hydrogen ion.
)into the alcohol and a hydrogen ion.
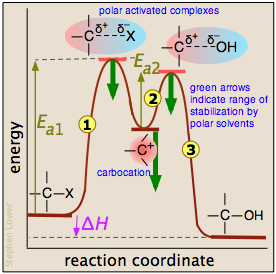
The reaction coordinate diagram helps us understand the effect of solvent polarity on this reaction. Polar solvent molecules interact most strongly with species in which the electric charge is concentrated in one spot. Thus the carbocation is stabilized to a greater degree than are the activated complexes in which the charge is spread out between the positive and negative ends. As the heavy green arrows indicate, a more polar solvent will stabilize the carbocation more than it will either of the activated complexes; the effect is to materially reduce the activation energy of the rate-determining step, and thus speed up the reaction. Because neither the alkyl chloride nor the alcohol is charged, the change in solvent polarity has no effect on the equilibrium constant of the reaction. This is dramatically illustrated by observing the rate of the reaction in solvents composed of ethanol and water in varying amounts:
| % water | 10 | 20 | 30 | 40 | 50 | 60 |
|---|---|---|---|---|---|---|
|
|
1.7 | 9.1 | 40.3 | 126 | 367 | 1294 |

