Catalytic Efficiency of Enzymes
- Page ID
- 1388
Enzymes exist in all biological systems in abundant numbers, but not all of their functions are fully understood. Enzymes are important for a variety of reasons, most significantly because they are involved in many vital biochemical reactions. Increasing the reaction rate of a chemical reaction allows the reaction to become more efficient, and hence more products are generated at a faster rate. These products then become involved in some other biological pathway that initiates certain functions of the human body. This is known as the catalytic efficiency of enzymes, which, by increasing the rates, results in a more efficient chemical reaction within a biological system.
Introduction
An enzyme's active sites are usually composed of amino acid residues; depending on which amino acid residues are present, the specificity of the substrate can vary greatly. Depending on the pH level, the physical properties (mainly the electric charge) of an enzyme can change. A change in the electric charge can alter the interaction between the active site amino acid residues and the incoming substrate. With that said, the substrate can bind to the active site via hydrogen bonding or van der Waals forces. Once the substrate binds to the active site it forms an enzyme-substrate complex that is then involved in further chemical reactions.
In order for an enzyme to be active and be energetically favorable to allow a chemical reaction to proceed forward, a substrate must bind to an enzyme's "active site". An active site can be thought of as a lock and the substrate as a key; this is known as the lock and key model. A key (substrate) must be inserted and turned (chemical reaction), then the lock (enzyme) opens (production of products). Note that an enzyme might have more than one active site. Another theory on the active site-substrate relationship is the induced fit theory, which is quite opposite of the lock and key theory (where the active site is seemingly inflexible). In the induced fit theory, the active site of the enzyme is very flexible, and only changes its conformation when the substrate binds to it.
Enzymes work as a catalyst by lowering the Gibbs free energy of activation of the enzyme-substrate complex. Below are two figures showing a basic enzymatic reaction with and without a catalyst:
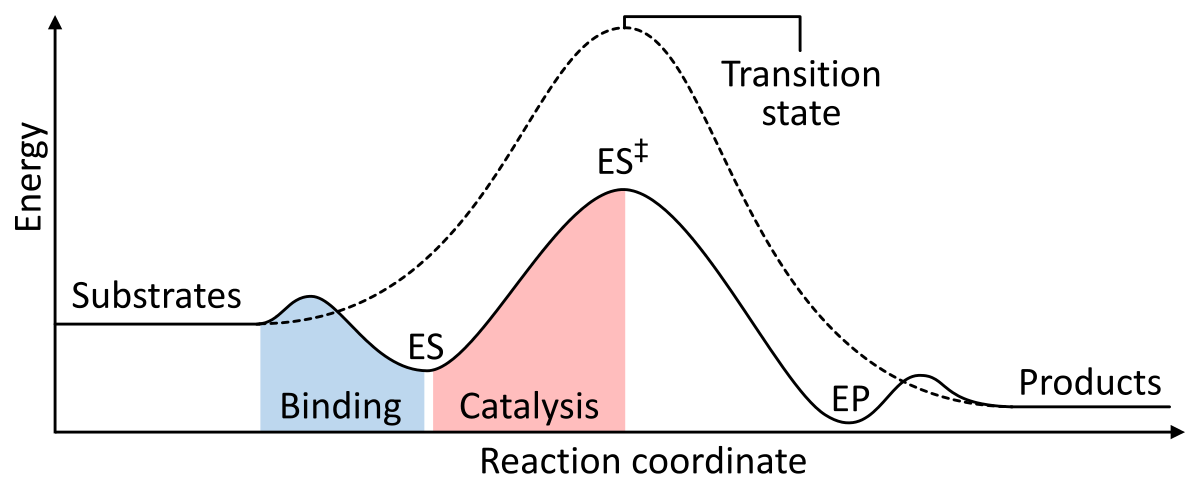
Figure 1: The energies of the stages of a chemical reaction. Uncatalyzed (dashed line), substrates need a lot of activation energy to reach a transition state, which then decays into lower-energy products. When enzyme catalyzed (solid line), the enzyme binds the substrates (ES), then stabilizes the transition state (ES‡) to reduce the activation energy required to produce products (EP) which are finally released. from Wikipedia.
The efficiency of the enzyme can be determined as follows: consider a simple enzymatic reaction:

German biochemist Leonor Michaelis and Canadian biochemist Maud Menten derived an equation describing this system, later known as the "Michaelis-Menten Equation", shown below:
\[ v_0 = \dfrac{V_{max}[S]}{K_M + [S]} \tag{1}\]
This equation gives the rate of the reaction at a given substrate concentration, assuming a known Vmax, which is the maximum rate the reaction can proceed at, and KM, the Michaelis constant. However, in a practical application of the Michaelis-Menten, V0 is often measured, and Vmax is observed as a saturation or plateau in a data plot. Because the substrate concentration is known, KM is usually the calculated value of interest.
For \(K_M\), assume \(V_0= \dfrac{V_{max}}{2}\):
\[\dfrac{V_{max}}{2} = \dfrac{V_{max}[S]}{K_M + [S]} \tag{2}\]
\[(K_M + [S]) \dfrac{V_{max}}{2} = V_{max}[S] \tag{3}\]
\[K_M + [S] = \dfrac{V_{max}[S]}{\dfrac{V_{max}}{2}} \tag{4} \]
\[K_M + [S] = 2[S] \tag{5}\]
\[ K_M = [S] \tag{6}\]
The Michaelis constant can be thought of as the rate at which the substrate becomes unbound from the enzyme, which can either occur in the events of substrate-enzyme complex becoming the product, or the substrate becomes unbound to the enzyme. KM can be shown as an equation.
\[ K_M = \dfrac{k_{-1} + k_2}{k_1} \tag{7} \]
Whereas k-1 is the rate constant at which the substrate becomes unbound to the enzyme, resulting in the dissociation of the enzyme-substrate complex, k2 is the rate constant where the substrate-enzyme complex disappears and turns into product, and K1 is the rate constant for the formation of the the substrate-enzyme complex formation. Therefore, KM can be viewed as the rate of substrate-enzyme complex disappearance divided by the rate of substrate-enzyme complex formation, which is the level at which half of the substrate is bound to the enzyme. KM is a useful indicator for the presence of an inhibitor because we can look for changes in KM and compare to our control (biological systems that we know have zero inhibitor presence). KM is a dependent variable, and its value can change due to many reasons, including the pH level of the system, temperature, or any other condition that might affect a chemical reaction. A small KM indicates that the substrate has a high affinity for the enzyme.
The Michaelis-Menten equation is most useful in measuring enzyme efficiency if v0 is plotted against [S], as follows:
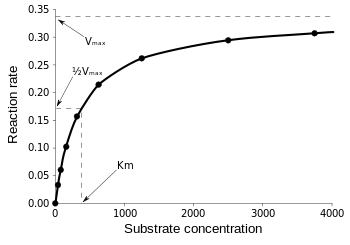
Figure 3: Diagram of reaction speed and Michaelis-Menten constant. from Wikipedia.
Vmax is the maximum rate at which the reaction can run, regardless of [S], meaning that even if you add more substrate, the reaction cannot go any faster. That is because at Vmax all of the active sites on the enzyme are occupied. After all the explanations on various forms of enzyme kinetic equations, we arrive at our conclusion of catalytic efficiency. Referring back to Fig 3, we have:
\[ V_o = k_2 \left(\dfrac{[E]_o[S]}{\dfrac{k_{-1} + k_2}{k_1} + [S]}\right) \tag{8}\]
Notice \(k_2\) describes an irreversible reaction as opposed to an equilibrium expression, when compared to k-1 and k1. k2 here is also known as kcat, the catalytic efficiency of enzyme. From the previous discussion, v0 is the measured reaction rate, which is the product formation over time, so it can be concluded that an equation would look like the following:
\[ v_0 = \dfrac{d[P]}{dt} = k_2[E]_0 \tag{9}\]
Where [E]0 is the total enzyme concentration.
It is also known that VMax is observed when all of the enzyme-substrate complex disappear and turn into products, so we can make the following assumption:
\[ V_{max} = k_2[E]_0 \tag{10} \]
and after rearrangement, we have this equation:
\[ k_{cat} = k_2 = \dfrac{V_{max} }{[E]_0} \tag{11}\]
That is the equation for calculating catalytic efficiency, to be used after we obtain data from experiments and after using the Michaelis-Menten equation. With a larger kcat , the enzyme is efficient because less enzyme is needed.
Problems
- What is the rate of product formation if k2 is 4.3 min-1 and [ES] is 2.3 x 10-2 M?
- Find the formation of ES if k1= 3.3 x 103 min-1, k-1 = 1.1 x 10-10 min-1 and [E] and [S] are 1.2 x 10-6 M and 6.3 x 10-2 M respectively.
- Given that k-1 = 8 x 104 s-1, k2 = 9 x 105 s-1, k1 = 7 x 106 M-1s-1 find KM. What does the answer tell us about the affinity of the substrate?
- Using the KM value from above, find v0 if we determine experimentally the Vmax value to be 1.5 x 10-4 M min-1 and the [S] is 5.1 x 10-4 M.
- Judging from KM from problem 1, we hypothesize that [E]0 is half of [S], find k2 using the Vmax value given above.

