Eddy Diffusion (Multipath) Broadening in Chromatography
- Page ID
- 70901
Consider a group of molecules flowing through a packed bed of particles (Figure 21). Another way to think of this is to imagine you and a group of friends following a river downstream in a set of inner tubes. The river has a number of rocks in the way and a variety of different flow paths through the rocks. Different people go in different channels either because they paddle over to them or get caught in different flows of the current as they bounce off of obstacles.
The question we need to consider is whether different molecules would have different path lengths as they passed through the bed. Would each person traveling down the river travel a slightly different distance, or would everyone travel the exact same distance? I suspect we can see that different molecules would end up traveling paths with different lengths as shown in Figure 22. One molecule (Molecule 1) might find a relatively straight shot through the packed bed, whereas another might encounter more particles that needed to be circumvented (Molecules 2 and 3). If we watched a group of molecules pass through a packed bed, and then mapped out each path with a length of string, we would see if we then stretched out all the strings, that there was a distribution of path lengths with some being shorter and some being longer. If that were the case, the molecule with the shortest path length would move through the column more quickly (Molecule 1). The molecule with the longest path length would move through the column more slowly (Molecule 3). If we have a distinction between the time it takes a set of molecules to move through the column based only on different path lengths, we have broadened the peak. This is known as eddy diffusion.
A key factor to consider when examining eddy diffusion is to ask whether the difference in length between the shortest and longest path depends at all on the diameter of the particles. If it is, we could then ask which particles (smaller or larger) would lead to a greater difference in path length?
Almost everyone who is asked the first question seems to intuitively realize that the size of the particles must somehow make a difference. It just seems too coincidental to think that the difference between the shortest and longest path would be identical if the particle sizes are different. But interestingly enough, almost everyone, when they first consider this, seems to select the wrong answer when figuring out which particle (small or large) would lead to a greater difference in path length between the shortest and longest path. Remember, the important distinction is the size of the difference between the shortest and longest path, not whether one column would uniformly have longer path lengths than the other.
To help with this assessment, two columns are pictured in Figure 23, one with small particles, the other with larger particles.
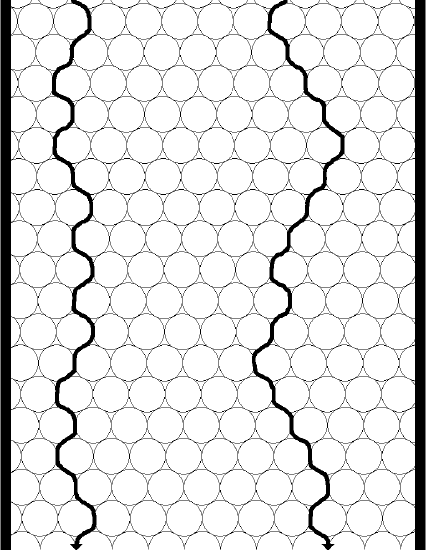
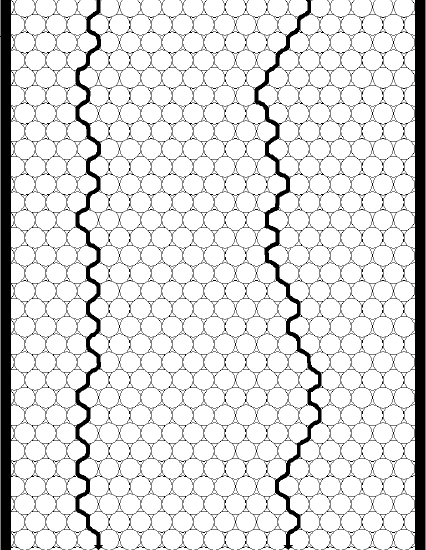
Note that the greatest distinction will occur between two molecules, one of which has found a relatively straight shot through the column, the other of which has encountered a lot of particles and so has to travel around them. Also note that the distance a molecule needs to travel around a larger particle is larger. Now you might be inclined to say that if we have to travel around lots of small particles, wouldn’t that eventually add up to the larger distance of travelling around one larger particle? Turns out that it doesn’t! The conclusion is that smaller particles will reduce the contribution of eddy diffusion to peak broadening (although we will add a proviso in just a bit). In other words, the distribution of path lengths of a set of molecules travelling through a packed bed is more uniform for a bed containing smaller particles than it is for a bed made up of larger particles. Thus, regarding eddy diffusion, there is a theoretical advantage to using smaller particles. That is the reason we use the reduced plate height (h = H/dp) instead of the plate height for an overall assessment of column efficiency. If we had two people pack a column with the idea of seeing who packed a better one, if one person used smaller particles they would have a competitive advantage if we only compared the plate height (H).
It is also worth realizing that the flow profile shown in Figure 24 for a molecule would not occur (okay, there’s probably some infinitesimally small possibility that this could occur, but it’s so small that we could ignore it) in a chromatographic column. There is a physical flow pushing the material through the column and when a molecule reaches a flowing area, it will generally be swept downstream.
Some packed columns exhibit channeling, and channeling leads to a significant and undesirable amount of eddy diffusion. The illustration in Figure 25 shows a column with a channel and compares two flow paths, one of which goes through the channel.
Channels provide a straight path through a portion of the column and molecules in a channel avoid any need to move around any particles. A molecule moving through a channel will have a much more streamlined or shorter path than a molecule in an adjacent part of the column that has to move through the packed bed. Channels occur when the particles stick together in some way and separate from each other, instead of nesting together in a packing arrangement with every particle closest together. A liquid chromatographic column that has dried out (all of the mobile phase is allowed to evaporate) will likely develop channels during the drying process that will never close back up if it is rewetted. Channels in chromatographic columns are undesirable and introduce a lot of broadening into the system.
Another key thing to ask then is whether channeling is more likely to occur with smaller or larger particles. Channeling will occur if a column is poorly packed. There are very specific procedures that have been developed for packing gas and liquid chromatographic columns that are designed to minimize the chance that channeling will occur. One key to packing a good column is to slowly lay down a bed of particles so that they nest into each other as well as possible. In packing a gas chromatographic column, this will usually involve slowly adding the particles to the column while vibrating it so that the particles settle in together. Liquid chromatographic columns are usually packed slowly under high pressure. A column is packed efficiently when the particles are in a uniform bed with the minimum amount of voids. Given a particular particle size, the goal is to fit as many of them as possible into the column. We can then ask which is more difficult to pack efficiently, larger or smaller particles.
One way to think about this is if you were asked to fill a large box (say a refrigerator box) with basketballs or tennis balls. The goal is to fit as many of either one in as possible. You could imagine readily taking the time to carefully lay down each basketball into the refrigerator box, layer by layer, and fitting in as many basketballs as possible. You might also be able to imagine that you would start slowly with the tennis balls, laying in one in a time, and quickly lose patience at how long this would take to fill the entire box. If you then sped up, say by slowing dumping in balls from a pail while a helper shook the box, you would probably create more voids in the box. Also, because the interstitial volumes between the tennis balls will be smaller than that with the basketballs, any channels become more significant. The result is that it is more difficult to avoid the formation of channels with smaller particles. Recapping, smaller particles have a theoretical advantage over larger particles, but more care must be exercised when packing smaller particles if this theoretical advantage in column efficiency is to be realized.
Do open tubular capillary columns exhibit eddy diffusion? Capillary columns do not have packing material. Instead, they are long, narrow diameter tubes that have a coating of a liquid stationary phase on the internal walls of the column. A representation of a capillary column with a uniform coating of a liquid on the walls is shown in Figure 26.
Because there is no packing material to move around, there would not be any eddy diffusion in such a column. The absence of eddy diffusion broadening is one advantage that capillary columns have when compared to packed columns.
Finally, we could ask whether eddy diffusion exhibits any dependence on the flow rate. This actually turns out to be a difficult question to answer with conflicting opinions and data about whether there is a flow dependence, and if so, exactly what the dependency is. If we go back to van Deemter’s initial development of peak broadening in chromatography in 1956, we would see that van Deemter believed that the contribution of eddy diffusion to peak broadening did not depend in any way on the flow rate. This is a reasonable argument if we thought that we could draw a variety of different flow paths through a packed bed, and the difference in length between the shortest and longest flow path would be fixed irrespective of how fast the molecules were moving through the path.
But let’s return to our river analogy to see how the flow rate might get involved in this. Suppose the river had a relatively fast flow rate, such that different people in different inner tubes got locked into particular flow channels and stayed in those all the way down the river. Under that situation, each path would have a preset length and even if we slowed down the flow, so long as you were locked into a particular path, the difference in distance would be invariant. But suppose now we slowed down the flow so much that there were opportunities to drift around at points and sample a variety of flow paths down the river. This might lead to some averaging and the amount of sampling of different flow paths would be greater the slower the flow. This same thing can happen in a chromatographic column and leads to conflicting data and opinions about the nature of any flow rate dependence on eddy diffusion. Also, the exact point at which there is a crossover between a rapid flow that locks in a flow path versus a slow one that allows each molecule to sample many different flow paths is impossible to determine. This point is still not fully resolved, and literature on band broadening show different terms for eddy diffusion. We usually denote eddy diffusion by the term A. If you look at van Deemter’s initial treatment of peak broadening, you would see (note, van Deemter also did not use the reduced plate height, but we could write h = A as well):
H = A
(where A = 2λdp)
Note how the particle diameter (dp) is included in this equation for A, so that the smaller the particle diameter, the smaller the contribution of eddy diffusion to the reduced plate height.
Another common conclusion today is that the contribution of eddy diffusion broadening does exhibit a slight dependence on flow rate. The usual form of this is that the dependence is v1/3, and you might often see books or articles that include the following term in the overall band broadening equation.
h = A v1/3
Still other people throw up their hands at all the confusion regarding eddy diffusion and show overall band broadening equations that do not have any A-term in them. We will develop another broadening term that has to do with processes going on in the mobile phase (and note that eddy diffusion only involves the mobile phase - none of what we talked about even requires the presence of a liquid stationary phase), so some people lump the eddy diffusion term into this other mobile phase term.


